Ang hanay ng mga numero na maihahambing sa a modulo m tinawag klase ng numero modulo m(o isang equivalence class). Ang lahat ng mga numero ng parehong klase ay may form mt+ r sa isang nakapirming r.

Para sa isang naibigay m, r maaaring tumagal ng mga halaga mula 0 hanggang m-1, ibig sabihin. lahat ng bagay ay umiiral m mga klase ng numero modulo m, at anumang integer ay mahuhulog sa isa sa mga klase na modulo m. Sa ganitong paraan,

Z= m m … [m-1]m, saan [ r]m={x Z: x≡r(mod m)}

Anumang bilang ng klase [ r]m tinawag minus modulo m na may paggalang sa lahat ng mga numero ng parehong klase. Ang numero ay katumbas ng natitira r, ay tinatawag na ang pinakamaliit na di-negatibong nalalabi.

Ang nalalabi na may pinakamaliit na ganap na halaga ay tinatawag ganap na hindi bababa sa deductible.

Halimbawa

Kunin natin ang modyul m=5. Bumitaw a=8. Hatiin natin a sa m kasama ang natitira:

Natitira r=3. Kaya 8 5 , at ang pinakamaliit na di-negatibong nalalabi ng 8 modulo 5 ay 3.

Ang ganap na pinakamaliit na nalalabi ay matatagpuan sa pamamagitan ng pagkalkula ng r-m=3-5=-2, at paghahambing ng mga ganap na halaga |-2| at |3|. |-2|<|3|, значит -2 – абсолютно наименьший вычет числа 8 по модулю 5.

Ang pagkuha ng isang bawas mula sa bawat klase, nakukuha namin kumpletong sistema ng pagsingil modulo m. Kung ang lahat ng mga numerong ito ay ang pinakamaliit na non-negatibong residues modulo m, kung gayon ang ganitong sistema ng mga nalalabi ay tinatawag kumpletong sistema ng hindi bababa sa mga hindi negatibong nalalabi, at tinutukoy ng Z m.

{0; 1;…; m-1) = Z m ay ang kumpletong sistema ng hindi bababa sa mga hindi negatibong nalalabi.

(– ;…; 0;…; ) (kung m-kakaibang numero);

( - ,…,-1, 0, 1,…, ) o (- ,…, -1, 0, 1,…, ) (kung m even number) ay isang kumpletong sistema ng ganap na hindi bababa sa mga nalalabi.

Halimbawa

Kung ang m=11, kung gayon ang kumpletong sistema ng hindi bababa sa hindi negatibong mga nalalabi ay (0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10), at ang kumpletong sistema ng ganap na hindi bababa sa mga nalalabi ay (-5). ; -4; -3 ; -2; -1; 0; 1; 2; 3; 4; 5).

Pahayag 1

Anuman m mga numero na magkapares na hindi maihahambing na modulo m, bumuo ng isang kumpletong sistema ng residues modulo ito.

Patunay:

Sa katunayan, dahil sa hindi pagkakatulad, ang mga numerong ito ay nabibilang sa iba't ibang klase, at mula noon sila m piraso, pagkatapos ay eksaktong isang numero ang nahuhulog sa bawat umiiral na klase.

Pahayag 2

Kung ang ( a, m) = 1, at x tumatakbo sa kumpletong sistema ng residues modulo m, pagkatapos palakol+b, saan b- anumang numero mula sa Z, ay tumatakbo din sa kumpletong sistema ng residues modulo m.

Patunay:

Numero palakol+b magiging eksakto m bagay. Ito ay nananatiling upang patunayan na ang anumang 2 numero palakol 1 +b at palakol 2 +b walang kapantay na modulo m, kung x 1 x 2 (mod m)

Patunay sa pamamagitan ng kontradiksyon. Magpanggap na tayo palakol 1 +b≡ palakol 2 +b(mod m) sa bisa ng ika-4 na paghahambing ng St.-va, palakol 1 ≡ palakol 2 (mod m) sa bisa ng mga paghahambing ng St-va No. 9 at ang katotohanan na ( a, m) = 1, mayroon kami x 1 ≡ x 2 (mod m). Nagkaroon tayo ng kontradiksyon sa katotohanang iyon x 1 x 2 (mod m). Samakatuwid, ang palagay ay mali, at samakatuwid ang kabaligtaran ay totoo. Yan ay palakol 1 +b at palakol 2 +b walang kapantay na modulo m, kung x 1 x 2 (mod m), na dapat patunayan.

Ang division equation () na tinalakay sa nakaraang seksyon ay may dalawang input (a at n) at dalawang output (q at r). Sa modular arithmetic, interesado lamang kami sa isa sa mga output, ang natitirang r. Wala kaming pakialam sa private q . Sa madaling salita, kapag hinati natin ang a sa n, interesado lang tayo sa kung ano ang halaga ng natitira ay r . Ito ay nagpapahiwatig na maaari naming katawanin ang imahe ng equation sa itaas bilang binary operator na may dalawang input a at n at isang output r .

Mga operasyon ng modulo

nabanggit binary operator pinangalanan modulo operator at tinutukoy bilang mod . Ang pangalawang input (n) ay pinangalanan modyul. Ang output r ay pinangalanan minus. Ipinapakita ng Figure 2.9 ang relasyon ng dibisyon laban sa modulo operator.

kanin. 2.9.

kanin. 2.13.

Sa katunayan, dalawang hanay ng mga operator ang ginagamit: ang unang hanay ay isa sa binary operator; ang pangalawa ay modulo operators. Dapat tayong gumamit ng mga panaklong upang bigyang-diin ang pagkakasunud-sunod ng gawain. Gaya ng ipinapakita sa fig. 2.13, ang mga input (a at b) ay maaaring mga miyembro ng Z o Z n .

Halimbawa 2.16

Isagawa ang mga sumusunod na pahayag (nagmula sa Z n ):

a. Pagdaragdag ng 7 at 14 sa Z 15

b. Ibawas ang 11 mula 7 hanggang Z 13

sa. I-multiply ang 11 sa 7 sa Z 20

Solusyon

(14+7) mod 15 -> (21) mod 15 = 6 (7–11) mod 13 -> (-4) mod 13 = 9 (7x11) mod 20 -> (77) mod 20 = 17

Halimbawa 2.17

Gawin ang mga sumusunod na operasyon (nanggagaling sa Z n ):

a. Pagdaragdag ng 17 at 27 sa Z 14

b. Ibawas ang 43 mula 12 hanggang Z 13

c. I-multiply ang 123 sa -10 sa Z 19

Solusyon

Ang dalawang hakbang para sa bawat operasyon ay ipinapakita sa ibaba:

(17 + 27) mod 14 -> (44) mod 14 = 2 (12 - 43) mod 13 -> (-31) mod 13 = 8 ((123) x (-10)) mod 19 -> (-1230 ) mod 19 = 5

Ari-arian

Nabanggit na natin na dalawang input para sa tatlo binary operator Ang paghahambing ng modulo ay maaaring gumamit ng data mula sa Z o Z n . Ang mga sumusunod na katangian ay nagbibigay-daan sa amin na imapa muna ang dalawang input sa Z n (kung nanggaling sila sa Z ) bago gawin ang tatlo

Mga klase sa pagbabawas. Mga sistema ng pagbabawas

Maikling impormasyon mula sa teorya

Gamit ang division theorem na may natitira, ang hanay ng mga integer ay maaaring hatiin sa isang bilang ng mga klase. Isaalang-alang ang isang halimbawa. Hayaan m = 6. Pagkatapos ay mayroon kaming anim na partition class ng set ng integers modulo 6:

r = 1;

r = 2;

r = 3;

r = 4;

r = 5;

kung saan saan r nagsasaad ng natitira sa isang buong bilang na hinati ng 6.

Alalahanin ang division theorem na may natitira:

Teorama: Hatiin ang isang numero sa isang numero , , na may natitira, pagkatapos ay maghanap ng isang pares ng mga integer q at r, upang ang mga sumusunod na kundisyon ay natutugunan: .

Madaling patunayan iyon para sa anumang integer a at ang paghahati na may natitira ay posible at mga numero q at r ay tinukoy nang hindi malabo. Sa aming halimbawa, ang kumpletong sistema ng hindi bababa sa mga hindi negatibong nalalabi ay ang set (0, 1, 2, 3, 4, 5); ang kumpletong sistema ng hindi bababa sa positibong residues ay ang set (0, 1, 2, 3, 4, 5); isang kumpletong sistema ng hindi bababa sa ganap na nalalabi - isang set (-2, -1, 0, 1, 2, 3); ang pinababang sistema ng mga nalalabi ay ang set (1,5), dahil ; factor-set

Ang isa sa mga pamamaraan para sa pagsasagawa ng mga operasyong aritmetika sa mga ibinigay na integer ay batay sa mga simpleng prinsipyo ng teorya ng numero. Ang ideya ng pamamaraang ito ay ang mga integer ay kinakatawan sa isa sa mga non-positional system - sa sistema ng mga natitirang klase. Namely: sa halip na mga operasyon sa mga integer, gumagana ang mga ito kasama ang mga natitira sa paghahati ng mga numerong ito sa pamamagitan ng mga pre-selected prime number - mga module .

Kadalasan ang mga numero pumili mula sa isang hanay ng mga prime number.

Hayaan …, .

Dahil ang division theorem na may natitira ay nagaganap sa singsing ng mga integer, ibig sabihin, kung saan , pagkatapos ay ang singsing Z, ayon sa kahulugan, ay Euclidean.

Kaya, bilang mga numero, maaari mong piliin ang mga natitira mula sa paghahati ng numero PERO sa p i ayon sa pagkakabanggit.

Binibigyang-daan ka ng residue system na magsagawa ng mga operasyon ng aritmetika sa isang may hangganan na hanay ng mga numero nang hindi lalampas dito. Kumpletong sistema ng mga pagbabawas modulo n ay anumang hanay ng n pairwise incomparable modulo n buong numero. Karaniwan bilang isang kumpletong sistema ng residues modulo n kunin ang pinakamaliit na di-negatibong nalalabi

Dibisyon ng integer a at m lumalabas na quotient q at ang natitira r , ganyan

a = m q + r, 0 r m-1. Natitira r tinawag DEDUKSYON ohm modulo m.

Halimbawa, para sa m = 3 at para sa m =5 nakukuha natin:

a = m q + r, m = 3	a = m q + r, m = 5
0 = 3 + 0	0 = 5 + 0
1 = 3 + 1	1 = 5 + 1
2 = 3 + 2	2 = 5 + 2
3 = 3 + 0	3 = 5 + 3
4 = 3 + 1	4 = 5 + 4
5 = 3 + 2	5 = 5 + 0
6 = 3 + 0	6 = 5 + 1
7 = 3 + 1	7 = 5 + 2

Kung ang natitira ay zero ( r=0 ), tapos sasabihin nila yan m naghahati a buo (o m maramihan a ), ibig sabihin m a , at ang mga numero q at m tinatawag na divisors a . Obvious naman 1 a at a a . Kung ang a walang ibang divisors kundi 1 at a , pagkatapos a ay isang prime number, kung hindi a tinatawag na composite number. Pinakamalaking positibong divisor d dalawang numero a at m tinatawag na greatest common divisor (GCD) at denote d = (a, m). Kung GCD (a,m)=1 , pagkatapos a at m walang mga karaniwang divisors maliban sa 1 , at sinasabing coprime na may paggalang sa isa't isa.

Sa bawat isa DEDUKSYON sa r = 0, 1, 2,…, m-1 tumutugma sa isang hanay ng mga integer a, b,... Sinasabi nila na ang mga numero ay may pareho DEDUKSYON ay modulo na maihahambing at tinutukoy ng isang b(mod m) o (a b) m .

Halimbawa, kapag m = 3 :

Halimbawa, kapag m = 5 :

Numero a , na maihahambing na modulo m , bumuo ng isang klase ng kanilang DEDUKSYON r at tinukoy bilang a = m q + r.

Numero a tinatawag din MGA DEDUKSYON modulo m . Hindi negatibo MGA DEDUKSYON a = r (sa q=0 ) pagkuha ng mga halaga mula sa pagitan , bumuo ng isang kumpletong sistema ng hindi bababa sa residues modulo m.

MGA DEDUKSYON a , pagkuha ng mga halaga mula sa pagitan [-( ,…,( ] , sa kakaiba m o mula sa pagitan [- sa kahit m bumuo ng isang kumpletong sistema ng ganap na pinakamaliit DEDUKSYON s modulo m.

Halimbawa, kapag m = 5 klase ng hindi bababa sa nalalabi na nabuo

r = 0, 1, 2, 3, 4, a = -2, -1, 0, 1, 2. Ang parehong ibinigay na hanay ng mga numero ay bumubuo ng mga kumpletong sistema bawas s modulo 5 .

Klase MGA DEDUKSYON, na ang mga elemento ay kasama ng module m

ay tinatawag na nabawasan. Tinutukoy ng Euler function kung magkano MGA DEDUKSYON mula sa kumpletong sistema ng hindi bababa sa residues modulo m sumama sa m . Kapag walang ginagawa m=p meron kami = p-1.

Kahulugan. Ang maximum na hanay ng pairwise incomparable modulo m mga numero na kasama ng m , ay tinatawag na pinababang sistema ng mga pagbabawas modulo m. Anumang pinababang sistema ng residues modulo m naglalaman ng mga elemento, kung saan ang Euler function.

Kahulugan. Anumang numero mula sa equivalence class єm tatawagan natin bawas ohm modulo m. Pinagsama-sama bawas s, kinuha ang isa mula sa bawat equivalence class єm, ay tinatawag na kumpletong sistema bawas s modulo m(sa buong sistema bawas ov, kaya kabuuan m piraso ng mga numero). Direkta ang mga natitira sa kanilang sarili kapag hinati sa m ay tinatawag na hindi bababa sa hindi negatibo bawas ami at, siyempre, bumuo ng isang kumpletong sistema bawas s modulo m. Pagbawas r ay tinatawag na absolutely smallest kung ang ïrï ang pinakamaliit sa mga module bawas s ng klase na ito.

Halimbawa. Suriin kung ang mga numero 13, 8, - 3, 10, 35, 60 ay bumubuo ng isang kumpletong sistema ng residues modulo m=6.

Solusyon: Sa pamamagitan ng kahulugan, ang mga numero ay bumubuo ng isang kumpletong sistema ng residues modulo m, kung may eksaktong m ng mga ito at sila ay magkapares na hindi maihahambing na modulo m.

Ang pairwise incomparability ay maaaring masuri sa pamamagitan ng pagpapalit sa bawat numero ng pinakamaliit na non-negative na nalalabi; kung walang mga pag-uulit, kung gayon ito ay isang kumpletong sistema ng mga pagbabawas.

Ilapat natin ang division theorem na may natitira: a = m q + r.

13 = 6 2 + 1 13 1(mod 6); 8 = 6 1 + 2 8 2(mod 6);

3 = 6 (-1) + 3 -3 3(mod 6); 10 = 6 1 + 4 10 4(mod 6);

35 = 6 5 + 5 35 5(mod 6); 60 = 6 10 + 0 60 0 (mod 6).

Nakakuha kami ng isang pagkakasunud-sunod ng mga numero: 1, 2, 3, 4, 5, 0, mayroong eksaktong 6 sa kanila, walang mga pag-uulit at ang mga ito ay magkapares na hindi maihahambing. Iyon ay, bumubuo sila ng isang kumpletong sistema ng mga residue modulo m = 6.

Halimbawa. Palitan ng pinakamaliit na absolute value, pati na rin ang pinakamaliit na positive residue 185 modulo 16.

Solusyon. Ilapat natin ang division theorem na may natitira:

185 = 16 11 + 9 185 9 (mod 16).

Halimbawa. Suriin kung nabuo ang mga numero (13, -13, 29, -9) ang pinababang sistema ng mga residue modulo m=10.

Solusyon: Anumang pinababang sistema ng residues modulo m naglalaman ng mga elemento, kung saan ang Euler function. Sa aming kaso =4, dahil kabilang sa mga natural na numero lamang 1, 3, 7, 9 ay medyo prime sa 10 at hindi lalampas dito. Ibig sabihin, posibleng ang apat na numerong ito ang bumubuo sa nais na sistema. Suriin natin ang mga numerong ito para sa kanilang pairwise incomparability: =4, dahil sa mga natural na numero ay 1, 3, 7, 9 lang ang relatibong prime hanggang 10 at hindi lalampas dito. Ibig sabihin, posibleng ang apat na numerong ito ang bumubuo sa nais na sistema. Suriin natin ang mga numerong ito para sa kanilang pairwise incomparability: m .

Opsyon 1. a= 185, m = 12; Opsyon 2. a = 84, m = 9;

Opsyon 3. a= 180, m = 10; Opsyon 4. a = 82, m = 9;

Opsyon 5. a= 85, m = 11; Pagpipilian 6. a = 84, m = 8;

Opsyon 7. a= 103, m = 87; Pagpipilian 8. a = 84, m = 16;

Opsyon 9. a= 15, m = 10; Opsyon 10. a = 81, m = 9;

Opsyon 11. a= 85, m = 15; Opsyon 12. a = 74, m = 13;

Opsyon 13. a= 185, m = 16; Opsyon 14. a = 14, m = 9;

Opsyon 15. a= 100, m = 11; Pagpipilian 16. a = 484, m = 15;

Opsyon 17. a= 153, m = 61; Opsyon 18. a = 217, m = 19;

Opsyon 19. a= 625, m = 25; Opsyon 20. a = 624, m = 25;

Gawain 3. Isulat ang kumpleto at pinababang sistema ng hindi bababa sa

Aytem 17. Kumpleto at binawasan ang mga sistema ng pagbabawas.

Sa nakaraang talata, nabanggit na ang ratio єm modulo ng comparability m ay isang katumbas na ugnayan sa hanay ng mga integer. Ang ugnayan ng equivalence na ito ay nag-uudyok ng partition ng set ng mga integer sa mga klase ng katumbas na elemento, i.e. ang mga numero ay pinagsama sa isang klase, na nagbibigay kapag hinati sa m ang parehong natira. Bilang ng mga klase ng equivalence єm(Sasabihin ng mga eksperto - "equivalence index єm") ay eksaktong katumbas ng m .

Kahulugan. Anumang numero mula sa equivalence class єm ay tatawaging residue modulo m. Set ng mga residues na kinuha ng isa mula sa bawat equivalence class єm, ay tinatawag na kumpletong sistema ng residues modulo m(sa buong sistema ng mga pagbabawas, samakatuwid, ang kabuuan m piraso ng mga numero). Direkta ang mga natitira sa kanilang sarili kapag hinati sa m ay tinatawag na hindi bababa sa hindi negatibong mga nalalabi at, siyempre, ay bumubuo ng isang kumpletong sistema ng mga residue modulo m. Ang isang residue r ay sinasabing ganap na pinakamaliit kung ang rp ay ang pinakamaliit sa mga residue module ng ibinigay na klase.

Halimbawa: Hayaan mo m= 5 . Pagkatapos:

0, 1, 2, 3, 4 - ang pinakamaliit na di-negatibong nalalabi;

Ang 2, -1, 0, 1, 2 ay talagang pinakamaliit na nalalabi.

Ang parehong pinababang hanay ng mga numero ay bumubuo ng kumpletong mga sistema ng residues modulo 5 .

Lemma 1. 1) Anuman m mga piraso sa pares na hindi maihahambing sa modulus m Ang mga numero ay bumubuo ng isang kumpletong sistema ng mga residue modulo m .

2) Kung a at m coprime, at xm, pagkatapos ay ang mga halaga ng linear form palakol+b, saan b- anumang integer, tumatakbo din sa kumpletong sistema ng residues modulo m .

Patunay. Assertion 1) ay halata. Patunayan natin ang assertion 2). Numero palakol+b makinis m bagay. Ipakita natin na hindi sila maihahambing sa bawat isa modulo m. Well hayaan para sa ilang mga iba't-ibang x 1 at x2 mula sa buong sistema ng mga pagbabawas ay lumabas na ax 1 +b є ax 2 +b(mod m). Pagkatapos, sa pamamagitan ng mga katangian ng mga paghahambing mula sa nakaraang talata, nakukuha natin:

palakol 1 - palakol 2 (mod m)

x 1 x 2 (mod m)

- isang kontradiksyon sa kung ano x 1 at x2 ay iba at kinuha mula sa buong sistema ng mga pagbabawas.

Dahil ang lahat ng mga numero mula sa isang ibinigay na equivalence class є ay nakuha mula sa isang numero ng isang ibinigay na klase sa pamamagitan ng pagdaragdag ng isang numero na isang multiple ng m, pagkatapos ang lahat ng mga numero mula sa klase na ito ay may modulo m ang parehong pinakamalaking karaniwang divisor. Para sa ilang kadahilanan, higit na interesado ang mga nalalabi na kasama ng module m ang pinakamalaking karaniwang divisor na katumbas ng isa, i.e. nalalabi na medyo prime sa modulus.

Kahulugan. Ang pinababang sistema ng residues modulo m ay ang hanay ng lahat ng nalalabi mula sa kumpletong sistema na may modulus m .

Ang pinababang sistema ay karaniwang pinipili mula sa pinakamaliit na hindi negatibong nalalabi. Ito ay malinaw na ang pinababang sistema ng residues modulo m naglalaman ng j ( m) mga piraso ng nalalabi, kung saan ang j ( m) ay ang Euler function, ang bilang ng mga numerong mas mababa sa m at sumama sa m. Kung sa puntong ito ay nakalimutan mo na ang pagpapaandar ng Euler, tingnan ang talata 14 at tiyaking may sinabi tungkol dito doon.

Halimbawa. Hayaan m= 42. Kung gayon ang pinababang sistema ng mga nalalabi ay:

1, 5, 11, 13, 17, 19, 23, 25, 29, 31, 37, 41.

Lemma 2. 1) Anumang j ( m) mga numero na magkapares na hindi maihahambing na modulo m at medyo prime sa modulus, bumuo ng isang pinababang sistema ng residues modulo m .

2) Kung (a, m) = 1 at x tumatakbo sa pamamagitan ng pinababang sistema ng residues modulo m, pagkatapos palakol tumatakbo din sa pamamagitan ng pinababang sistema ng residues modulo m .

Patunay. Assertion 1) ay halata. Patunayan natin ang assertion 2). Numero palakol ay magkapares na hindi maihahambing (ito ay napatunayan sa parehong paraan tulad ng sa Lemma 1 ng subsection na ito), mayroong eksaktong j ( m) bagay. Malinaw din na lahat sila ay medyo prime sa module, dahil (a,m)=1, (x,m)=1 X (ax.m)=1. Kaya ang mga numero palakol bumuo ng pinababang sistema ng mga pagbabawas.

Ito ang mga kahulugan at pangunahing katangian ng buo at pinababang mga sistema ng mga nalalabi, gayunpaman, sa bagahe ng kaalaman sa matematika ay mayroon pa ring isang bilang ng mga napaka-kawili-wili at kapaki-pakinabang na mga katotohanan tungkol sa mga sistema ng mga nalalabi. Kung manahimik tayo tungkol sa mga ito sa talatang ito, kung gayon ito, natatakot ako, ay magiging isang direktang paglabag sa Batas ng Russian Federation sa Impormasyon, ang malisyosong pagtatago kung saan, ayon sa batas na ito, ay isang administratibo at kahit na may parusang kriminal. kumilos. Bilang karagdagan, nang walang pamilyar sa karagdagang mahahalagang katangian ng mga sistema ng pagbabawas, ang talata 17 ay magiging napakaikli. Ituloy natin.

Lemma 3. Hayaan m 1 , m 2 , ..., m k ay pairwise coprime at m 1 m 2 ...m k =M 1 m 1 =M 2 m 2 =...=M k m k, saan

1) Kung x 1 , x 2 , ..., x k tumakbo sa pamamagitan ng kumpletong mga sistema ng residues modulo m 1 , m 2 , ..., m k tumakbo sa kumpletong sistema ng residues modulo m=m 1 m 2 ...m k .

2) Kung x 1 , x 2 , ..., x k tumakbo sa mga pinababang sistema ng residues modulo m 1 , m 2 , ..., m k ayon sa pagkakabanggit, pagkatapos ay ang mga halaga ng linear form tumakbo sa pamamagitan ng pinababang sistema ng residues modulo m=m 1 m 2 ...m k .

Patunay.

1) Form M 1 x 1 +M 2 x 2 + ...+M k x k halatang tumatagal m 1 m 2 ...m k =m mga halaga. Ipakita natin na ang mga halagang ito ay magkapares na hindi maihahambing. Well hayaan

M 1 x 1 +M 2 x 2 + ...+M k x k є M 1 x 1 C +M 2 x 2 C + ...+M k x k C (mod m)

Anumang bagay Mj, Iba sa MS, maramihan MS. Ang pag-alis ng kaliwa at kanang termino sa huling paghahambing, mga multiple ng MS, nakukuha natin ang:

M s x s є M s x s C (mod m s) Yu x s ​​​​є x s C (mod m s)

- isang kontradiksyon sa kung ano x s tumatakbo sa kumpletong sistema ng residues modulo MS .

2). Ang porma M 1 x 1 +M 2 x 2 + ...+M k x k halatang kumukuha ng j ( m 1) j ( m2) Ch ... Ch j ( m k) = j ( m 1 m 2 W ... W m k)= j ( m) (ang Euler function ay multiplicative!) ng iba't ibang mga halaga, na modulo m=m 1 m 2 ...m k magkapares na walang kapantay. Ang huli ay madaling patunayan ng mga argumentong katulad ng ginamit sa patunay ng assertion 1) nitong lemma. kasi ( M 1 x 1 +M 2 x 2 + ...+M k x k ,m s)=(M s x s ,m s)=1 para sa lahat 1 J s J k, pagkatapos ( M 1 x 1 +M 2 x 2 + ...+M k x k ,m s)=1, samakatuwid ang hanay ng mga halaga ng form M 1 x 1 +M 2 x 2 + ...+M k x k bumubuo ng isang pinababang sistema ng residues modulo m .

Lemma 4. Hayaan x 1 , x 2 , ..., xk ,x tumakbo nang buo, at x 1 , x 2 ,..., x k , x– tumakbo sa mga pinababang sistema ng mga nalalabi sa mga module m 1 , m 2 , ..., m k at m=m 1 m 2 ...m k ayon sa pagkakabanggit, kung saan (m i m j)=1 sa ako № j. Tapos fractions tugma sa mga fraction (x/m), at mga fraction tugma sa mga fraction (x/m) .

Patunay. Ang patunay ng parehong mga pahayag ng Lemma 4 ay madaling makuha sa pamamagitan ng paglalapat ng nakaraang Lemma 3 pagkatapos mong ibigay ang bawat kabuuan (x 1 /m 1 +x 2 /m 2 +...+x k /m k ) at ( x 1 /m 1 + x 2 /m 2 +...+ x k /m k ) sa isang karaniwang denominator:

(x 1 /m 1 +x 2 /m 2 +...+x k /m k )=((M 1 x 1 +M 2 x 2 +...+M k x k)/m) ;

( x 1 /m 1 + x 2 /m 2 +...+ x k /m k )=((M 1 x 1 +M 2 x 2 +...+M k x k)/m) ,

saan M j =m 1 ...m j-1 m j+1 ...m k .

Kung isasaalang-alang natin ngayon na ang mga fractional na bahagi ng mga numero na nakuha sa pamamagitan ng paghati sa modulus m anumang dalawang numero na maihahambing sa modulus m, ay pareho (pareho sila r/m, saan r ay ang pinakamaliit na di-negatibong nalalabi mula sa ibinigay na klase), kung gayon ang mga pahayag ng kasalukuyang lemma ay nagiging halata.

Sa natitirang bahagi ng seksyong ito, ang pinaka-kagiliw-giliw na bagay ay mangyayari - ibubuod natin ang mga kumplikadong ugat m kapangyarihan mula sa pagkakaisa, at matutuklasan natin ang mga kamangha-manghang koneksyon sa pagitan ng mga root sums, residue system, at ang pamilyar nang multiplicative Möbius function m ( m) .

Tukuyin ng e k k-ika-ugat m- oh degree mula sa pagkakaisa:

Naaalala namin ang mga paraan ng pagsulat ng mga kumplikadong numero nang maayos mula sa unang taon. Dito k=0,1,...,m-1– tumatakbo sa kumpletong sistema ng residues modulo m .

Tandaan na ang halaga e 0 + e 1 +...+ e m-1 lahat ng ugat m ang kapangyarihan ng pagkakaisa ay zero para sa alinman m. Sa katunayan, hayaan e 0 + e 1 +...+ e m-1 =a. I-multiply natin ang kabuuan na ito sa isang di-zero na numero e 1 . Ang ganitong multiplikasyon geometrically sa kumplikadong eroplano ay nangangahulugan ng pag-ikot ng tama m-gon, sa mga vertice kung saan matatagpuan ang mga ugat e 0 , e 1 ,..., e m-1, sa isang di-zero na anggulo 2p/m. Ito ay malinaw na sa kasong ito ang ugat e 0 pumunta sa ugat e 1, ugat e 1 pumunta sa ugat e 2, atbp., at ang ugat e m-1 pumunta sa ugat e 0, ibig sabihin. sum e 0 + e 1 +...+ e m-1 Hindi magbabago. Meron kami e 1 a=a, saan a=0 .

Teorama 1. Hayaan m>0- isang integer, isang O Z , x tumatakbo sa kumpletong sistema ng residues modulo m. Tapos kung a maramihan m, pagkatapos

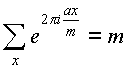
kung hindi, kapag a hindi maramihan m ,

.

Patunay. Sa a maramihan m meron kami: a=md at

Sa a hindi mahahati ng m, hatiin ang numerator at denominator ng fraction a/m sa d ay ang pinakamalaking karaniwang divisor a at m, nakakakuha tayo ng hindi mababawasang bahagi isang 1 /m 1. Pagkatapos, sa pamamagitan ng Lemma 1, isang 1 x ay tatakbo sa kumpletong sistema ng residues modulo m. Meron kami:

dahil ang kabuuan ng lahat ng mga ugat ng antas m 1 mula sa pagkakaisa ay katumbas ng zero.

Tandaan na ang ugat e k m Ang kapangyarihan ng pagkakaisa ay tinatawag na antiderivative kung ang index nito k kapwa simple sa m. Sa kasong ito, tulad ng napatunayan sa unang taon, sunud-sunod na degree e k 1 , e k 2 ,..., e k m-1 ugat e k bumuo ng buong hanay ng mga ugat m kapangyarihan mula sa pagkakaisa o, sa madaling salita, e k ay isang generator ng cyclic group ng lahat ng mga ugat m ika-degree mula sa pagkakaisa.

Malinaw, ang bilang ng iba't ibang mga primitive na ugat m ang kapangyarihan ng pagkakaisa ay katumbas ng j ( m), kung saan ang j ay ang Euler function, dahil ang mga indeks sa primitive roots ay bumubuo ng isang pinababang sistema ng residues modulo m .

Teorama 2. Hayaan m>0 ay isang integer, x ay tumatakbo sa pinababang sistema ng residues modulo m. Pagkatapos (ang kabuuan ng mga primitive na ugat ng degree m):

saan m ( m) ay ang function ng Möbius.

Patunay. Hayaan m=p 1 a 1 p 2 a 2 ...p k a k ay ang kanonikal na pagpapalawak ng bilang m ; m 1 \u003d p 1 a 1 , m 2 \u003d p 2 a 2 , m 3 \u003d p 3 a 3; x i tumatakbo sa pamamagitan ng pinababang sistema ng residues modulo m i. Meron kami:

Sa a s =1 ugat lang pala e 0 =1 ay hindi primitive, kaya ang kabuuan ng lahat ng primitive na ugat ay ang kabuuan ng lahat ng ugat minus isa:

kaya kung m libre mula sa mga parisukat (i.e. hindi nahahati ng r2, sa r>1), pagkatapos

Kung may indicator isang s higit sa isa (i.e. m hinati ng r2, sa r>1), pagkatapos ay ang kabuuan ng lahat ng primitive na ugat ng degree MS ay ang kabuuan ng lahat ng mga ugat ng antas MS bawasan ang kabuuan ng lahat ng di-primitive na ugat, i.e. lahat ng mga ugat ng ilang antas na mas mababa MS. Eksakto, kung m s =p s m s *, pagkatapos:

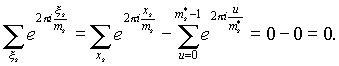
Ngayon, mahal na mga mambabasa, kapag iniharap ko para sa iyong pagsasaalang-alang ang isang medyo makabuluhang halaga ng impormasyon tungkol sa buo at pinababang mga sistema ng pagbabawas, walang sinuman ang maaaring akusahan ako ng malisyosong paglabag sa Batas ng Russian Federation sa Impormasyon sa pamamagitan ng pagpigil nito, kaya tapusin ko ito talata nang may kasiyahan.

mga palaisipan

1 . Isulat sa isang piraso ng papel ang lahat ng pinakamaliit na hindi negatibong nalalabi at lahat ng ganap na pinakamaliit na nalalabi a) modulo 6, b) modulo 8. Sa ibaba lamang, isulat ang ibinigay na mga sistema ng pagbabawas para sa mga modyul na ito. Iguhit nang hiwalay sa kumplikadong eroplano ang mga ugat ng ikaanim at ang ikawalong ugat ng pagkakaisa, sa parehong mga pigura ay bilugan ang mga primitive na ugat at hanapin sa bawat kaso ang kanilang kabuuan. 2 . Hayaan e- primitive na ugat 2n mula sa isang unit. Hanapin ang halaga: 1+ e + e 2 +...+ e n-1 . 3 . Hanapin ang kabuuan ng lahat ng primitive na ugat: a) ika-15; b) ika-24; c) ika-30 antas mula sa pagkakaisa. 4 . Hanapin ang kabuuan ng lahat ng posibleng produkto ng mga primitive na ugat n ika degree mula sa isa, kinuha ng dalawa. 5 . hanapin ang kabuuan k-x kapangyarihan ng lahat ng mga ugat n ika-degree mula sa pagkakaisa. 6 . Hayaan m>1 , (a, m)=1 , b ay isang integer, X tumatakbo sa kumpleto at x tumatakbo sa pinababang sistema ng residues modulo m. Patunayan na: a) b) 7 . Patunayan na: , saan R tumatakbo sa lahat ng prime divisors ng isang numero a .

Kumpletuhin ang sistema ng pagsingil. Ang ibinigay na sistema ng mga pagbabawas. Ang pinakakaraniwang mga sistema ng pagbabawas ay: hindi bababa sa positibo, hindi bababa sa hindi negatibo, ganap na hindi bababa sa, atbp.

Teorama 1. Mga katangian ng kumpleto at pinababang sistema ng mga nalalabi.

1°. Pamantayan para sa kumpletong sistema ng mga pagbabawas. Anumang kumbinasyon ng m mga integer na magkapares na walang kapantay na modulo m, ay bumubuo ng isang kumpletong sistema ng residues modulo m.

2°. Kung mga numero x 1 , x 2 , ..., x m– kumpletong sistema ng residues modulo m, (a, m) = 1, b ay isang arbitrary integer, pagkatapos ay ang mga numero palakol 1 +b, palakol 2 +b, ..., palakol m+b bumubuo rin ng isang kumpletong sistema ng residues modulo m.

3°. Pamantayan ng Sistema ng Pinababang Pagbawas. Anumang koleksyon na binubuo ng j( m) mga integer na magkapares na walang kapantay na modulo m at coprime sa modulus, ay bumubuo ng isang pinababang sistema ng residues modulo m.

4°. Kung mga numero x 1 , x 2 , ..., x j ( m) ay ang pinababang sistema ng residues modulo m, (a, m) = 1, pagkatapos ay ang mga numero palakol 1 , palakol 2 , ..., isang x j ( m) ay bumubuo rin ng pinababang sistema ng mga residue modulo m.

Teorama 2. Ang teorama ni Euler.

Kung mga numero a at m coprime, kung gayon a j ( m) º 1(mod m).

Bunga.

1°. Teorama ni Fermat. Kung ang p ay isang prime number at a hindi mahahati ng p, pagkatapos isang p–1 º 1(mod p).

2°. Pangkalahatan ang teorama ni Fermat. Kung ang p ay isang prime number, kung gayon isang p º a(mod p) para sa alinman aÎ Z .

§ apat. Paglutas ng mga paghahambing sa isang variable

Paghahambing ng desisyon. Pagkakapantay-pantay. Ang antas ng paghahambing.

Teorama. Mga katangian ng mga solusyon ng mga congruence.

1°. Ang mga solusyon ng mga congruence ay mga buong klase ng mga nalalabi.

2°. (" k)(isang k º b k(mod m))Ù k= z ng paghahambing º 0 (mod m) at º 0 (mod m) ay katumbas.

3°. Kung ang parehong bahagi ng paghahambing ay pinarami ng isang numero na coprime sa modulus, pagkatapos ay makakakuha tayo ng isang paghahambing na katumbas ng orihinal.

4°. Anumang paghahambing modulo a prime p ay katumbas ng isang paghahambing, ang antas nito ay hindi lalampas p–1.

5°. Paghahambing º 0 (mod p), saan p ay isang prime number, may pinakamarami n iba't ibang solusyon.

6°. Ang teorama ni Wilson. ( n-isa)! º –1 (mod n) Û n Prime number.

§ 5. Paglutas ng mga paghahambing ng unang antas

palakol º b(mod m).

Teorama. 1°. Kung ang ( a, m) = 1, kung gayon ang paghahambing ay may solusyon, at ito ay natatangi.

2°. Kung ang ( a, m) = d at b hindi mahahati ng d, kung gayon ang paghahambing ay walang mga solusyon.

3°. Kung ang ( a, m) = d at b hinati ng d, pagkatapos ay mayroon ang paghahambing d iba't ibang solusyon na bumubuo sa isang klase ng modulo residues.

Mga paraan upang malutas ang mga paghahambing palakol º b(mod m) kailan ( a, m) = 1:

1) pagpili (enumeration ng mga elemento ng isang kumpletong sistema ng mga pagbabawas);

2) paggamit ng teorama ni Euler;

3) paggamit ng Euclid algorithm;

4) pagkakaiba-iba ng mga coefficients (gamit ang property 2° ng kumpletong sistema ng residues mula sa Theorem 2.2);

§6. Hindi tiyak na mga equation ng unang antas

palakol+sa pamamagitan ng = c.

Teorama. Ang equation palakol+sa pamamagitan ng = c malulutas kung at kung lamang c (a, b).

Kailan ( a, b) = 1 lahat ng mga solusyon ng equation ay ibinibigay ng mga formula

tÎ Z , saan x 0 ay ilang solusyon sa paghahambing

palakol º c(mod b), y 0 = .

Mga equation ng diophantine.

KABANATA 10. Mga kumplikadong numero

Kahulugan ng isang sistema ng mga kumplikadong numero. Pagkakaroon ng isang sistema ng mga kumplikadong numero

Kahulugan ng isang sistema ng mga kumplikadong numero.

Teorama. Ang sistema ng mga kumplikadong numero ay umiiral.

modelo: R 2 na may mga operasyon

(a, b)+(c, d) = (a+c, b+d), (a, b)×( c, d) = (ac–bd, bc+Ad),

i= (0, 1) at pagkakakilanlan a = (a, 0).

Algebraic na anyo ng isang kumplikadong numero

Representasyon ng isang kumplikadong numero sa anyo z = a+bi, saan a, bÎ R , i 2 = -1. Ang kakaiba ng naturang representasyon. Re z, Im z.

Mga panuntunan para sa pagsasagawa ng mga pagpapatakbo ng aritmetika sa mga kumplikadong numero sa algebraic form.

Arithmetic n-dimensional na espasyo ng vector C n. Tapos na ang mga sistema ng linear equation, matrice at determinants C .

Pagkuha ng mga square root mula sa mga kumplikadong numero sa algebraic form.
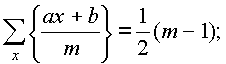