bilan taqqoslanadigan raqamlar to'plami a modul m chaqirdi raqam sinfi modul m(yoki ekvivalent sinf). Xuddi shu sinfning barcha raqamlari shaklga ega mt+ r belgilangan vaqtda r.

Berilgan uchun m, r 0 dan qiymatlarni qabul qilishi mumkin m-1, ya'ni. hamma narsa mavjud m raqamli sinflar moduli m, va har qanday butun son modul sinflaridan biriga tushadi m. Shunday qilib,

Z= m m … [m-1]m, qaerda [ r]m={x Z: x≡r(mod m)}

Har qanday sinf soni [ r]m chaqirdi minus modul m bir xil sinfning barcha raqamlariga nisbatan. Raqam qolganga teng r, deyiladi eng kichik manfiy bo'lmagan qoldiq.

Eng kichik mutlaq qiymatga ega bo'lgan qoldiq deyiladi mutlaqo eng kam chegirib tashlanadi.

Misol

Keling, modulni olaylik m=5. Qo'yib yubor a=8. Keling, ajratamiz a ustida m qolganlari bilan:

Qolgan r=3. Shunday qilib, 8 5 va 8 modul 5 ning eng kichik manfiy bo'lmagan qoldig'i 3 ga teng.

Mutlaq eng kichik qoldiqni r-m=3-5=-2 hisoblash va mutlaq qiymatlarni solishtirish orqali topish mumkin |-2| va |3|. |-2|<|3|, значит -2 – абсолютно наименьший вычет числа 8 по модулю 5.

Har bir sinfdan bitta chegirma olib, biz olamiz to'liq hisob-kitob tizimi modul m. Agar bu raqamlarning barchasi eng kichik manfiy bo'lmagan qoldiqlar moduli bo'lsa m, keyin bunday qoldiqlar tizimi deyiladi eng kam salbiy bo'lmagan qoldiqlarning to'liq tizimi, va Z bilan belgilanadi m.

{0; 1;…; m-1) = Z m eng kam manfiy bo'lmagan qoldiqlarning to'liq tizimidir.

(– ;…; 0;…; ) (agar m-toq raqam);

( - ,…,-1, 0, 1,…, ) yoki (- ,…, -1, 0, 1,…, ) (agar m juft son) - mutlaqo eng kam qoldiqlarning to'liq tizimi.

Misol

Agar m=11, u holda eng kam manfiy bo'lmagan qoldiqlarning to'liq tizimi (0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10) va mutlaqo eng kichik qoldiqlarning to'liq tizimi (-5) ga teng. ; -4; -3; -2; -1; 0; 1; 2; 3; 4; 5).

Bayonot 1

Har qanday m juftlik bilan taqqoslanmaydigan modul bo'lgan raqamlar m, bu modulga qoldiqlarning to'liq tizimini tashkil qiladi.

Isbot:

Haqiqatan ham, taqqoslanmasligi sababli, bu raqamlar turli sinflarga tegishli va shundan beri ular m dona, keyin har bir mavjud sinfga aynan bitta raqam tushadi.

Bayonot 2

Agar ( a, m) = 1, va x qoldiq modulining to'liq tizimidan o'tadi m, keyin bolta+b, qayerda b- Z dan istalgan raqam, shuningdek, modulli qoldiqlarning to'liq tizimidan o'tadi m.

Isbot:

Raqamlar bolta+b aynan bo'ladi m narsalar. Har qanday 2 raqam ekanligini isbotlash uchun qoladi bolta 1 +b Va bolta 2 +b tengsiz modul m, agar x 1 x 2 (mod m)

Qarama-qarshilik bilan isbotlash. Keling, shunday da'vo qilaylik bolta 1 +b≡ bolta 2 +b(mod m) 4-St.-va taqqoslashlari tufayli, bolta 1 ≡ bolta 2 (mod m) 9-sonli St-va taqqoslashlari tufayli va ( a, m) = 1, bizda bor x 1 ≡ x 2 (mod m). Bizda bu bilan qarama-qarshilik bor x 1 x 2 (mod m). Shuning uchun, taxmin noto'g'ri va shuning uchun teskari haqiqatdir. Ya'ni bolta 1 +b Va bolta 2 +b tengsiz modul m, agar x 1 x 2 (mod m), bu isbotlanishi kerak edi.

Oldingi bo'limda muhokama qilingan bo'linish tenglamasi () ikkita kirish (a va n) va ikkita chiqish (q va r) ga ega. Modulli arifmetikada bizni faqat natijalardan biri qiziqtiradi, qolgan r. Bizni shaxsiy q qiziqtirmaydi. Boshqacha qilib aytganda, a ni n ga bo'lganimizda, bizni faqat nima qiziqtiradi qolgan qismining qiymati r. Bu yuqoridagi tenglamaning tasvirini quyidagicha ifodalashimiz mumkinligini anglatadi ikkilik operator ikkita kirish a va n va bitta chiqish r bilan.

Modul operatsiyalari

yuqorida aytib o'tilgan ikkilik operator nomli modul operatori va mod sifatida belgilanadi. Ikkinchi kirish (n) nomi berilgan modul. Chiqish r nomlanadi minus. 2.9-rasmda modul operatoriga bo'linishning munosabati ko'rsatilgan.

Guruch. 2.9.

Guruch. 2.13.

Aslida, ikkita operatorlar to'plami ishlatiladi: birinchi to'plam ulardan biri ikkilik operatorlar; ikkinchisi modul operatorlari. Ish tartibini ta'kidlash uchun qavslardan foydalanishimiz kerak. Shaklda ko'rsatilganidek. 2.13, kirishlar (a va b) Z yoki Z n a'zolari bo'lishi mumkin.

2.16-misol

Quyidagi gaplarni bajaring (Z n dan kelib chiqadi):

lekin. Z 15 ga 7 va 14 ni qo‘shish

b. 7 dan Z 13 ga 11 ni ayiring

ichida. Z 20 da 11 ni 7 ga ko'paytiring

Yechim

(14+7) mod 15 -> (21) mod 15 = 6 (7–11) mod 13 -> (-4) mod 13 = 9 (7x11) mod 20 -> (77) mod 20 = 17

2.17-misol

Quyidagi amallarni bajaring (Z n dan keladi):

a. Z 14 ga 17 va 27 qo'shilishi

b. 12 dan Z 13 ga 43 ni ayiring

c. Z 19 da 123 ni -10 ga ko‘paytiring

Yechim

Har bir operatsiya uchun ikkita qadam quyida ko'rsatilgan:

(17 + 27) mod 14 -> (44) mod 14 = 2 (12 - 43) mod 13 -> (-31) mod 13 = 8 ((123) x (-10)) mod 19 -> (-1230) ) mod 19 = 5

Xususiyatlari

Biz allaqachon uchta uchun ikkita kirishni aytib o'tgan edik ikkilik operatorlar modullarni taqqoslash Z yoki Z n ma'lumotlaridan foydalanishi mumkin. Quyidagi xususiyatlar uchta kirishni amalga oshirishdan oldin ikkita kirishni Z n ga (agar ular Z dan kelgan bo'lsa) xaritalash imkonini beradi.

Deduktsiya sinflari. Deduksiya tizimlari

Nazariyadan qisqacha ma'lumot

Qoldiq bilan bo'lish teoremasidan foydalanib, butun sonlar to'plamini bir qancha sinflarga bo'lish mumkin. Bir misolni ko'rib chiqing. Bo'lsin m = 6. Keyin bizda modul 6 butun sonlar to'plamining oltita bo'linish sinfi mavjud:

r = 1;

r = 2;

r = 3;

r = 4;

r = 5;

qayerdan orqali r 6 ga bo'lingan butun sonning qolgan qismini bildiradi.

Qoldiq bilan bo'linish teoremasini eslang:

Teorema: Sonni , , qoldiq bilan songa bo'ling, so'ngra butun sonlar juftini toping q Va r, shunday qilib, quyidagi shartlar bajariladi: .

Har qanday butun sonlar uchun buni isbotlash oson lekin va qoldiq bilan bo'lish mumkin va raqamlar q Va r aniq belgilangan. Bizning misolimizda eng kam manfiy bo'lmagan qoldiqlarning to'liq tizimi to'plamdir (0, 1, 2, 3, 4, 5); eng kam ijobiy qoldiqlarning to'liq tizimi to'plamdir (0, 1, 2, 3, 4, 5); eng kam mutlaq qoldiqlarning to'liq tizimi - to'plam (-2, -1, 0, 1, 2, 3); qoldiqlarning qisqartirilgan tizimi to'plam (1,5), chunki ; omillar to'plami

Berilgan butun sonlar ustida arifmetik amallarni bajarish usullaridan biri sonlar nazariyasining oddiy tamoyillariga asoslanadi. Ushbu usulning g'oyasi shundaki, butun sonlar pozitsiyali bo'lmagan tizimlardan birida - qoldiq sinflar tizimida ifodalanadi. Ya'ni: butun sonlar ustidagi amallar o'rniga ular bu raqamlarni oldindan tanlangan tub sonlarga bo'lish qoldiqlari - modullar bilan ishlaydi. .

Ko'pincha raqamlar tub sonlar to‘plamidan tanlang.

Bo'lsin …, .

Qoldiq bilan bo'linish teoremasi butun sonlar halqasida sodir bo'lganligi sababli, ya'ni qaerda , keyin halqa. Z, ta'rifiga ko'ra, Evkliddir.

Shunday qilib, raqamlar sifatida siz raqamni bo'lishdan qolganlarni tanlashingiz mumkin LEKIN ustida p i mos ravishda.

Qoldiqlar tizimi cheklangan sonlar to'plamida undan tashqariga chiqmasdan arifmetik amallarni bajarishga imkon beradi. Chegirmalarning to'liq tizimi modul n har qanday to'plamdir n juftlik bilan taqqoslanmaydigan modul n butun sonlar. Odatda modulli qoldiqlarning to'liq tizimi sifatida n eng kichik salbiy bo'lmagan qoldiqlarni oling

Butun sonlarni bo'lish a Va m ko'rsatkich bo'lib chiqadi q va qolganlari r , shu kabi

a = m q + r, 0 r m-1. Qolgan r chaqirdi CHEKIRISH ohm moduli m.

Masalan, uchun m = 3 va uchun m =5 biz olamiz:

a = m q + r, m = 3	a = m q + r, m = 5
0 = 3 + 0	0 = 5 + 0
1 = 3 + 1	1 = 5 + 1
2 = 3 + 2	2 = 5 + 2
3 = 3 + 0	3 = 5 + 3
4 = 3 + 1	4 = 5 + 4
5 = 3 + 2	5 = 5 + 0
6 = 3 + 0	6 = 5 + 1
7 = 3 + 1	7 = 5 + 2

Qolgan nolga teng bo'lsa ( r=0 ), keyin shunday deyishadi m ajratadi a butun (yoki m bir nechta a ), bu degani m a , va raqamlar q Va m bo'luvchilar deyiladi a . Shubhasiz 1 a Va a a . Agar a dan boshqa boʻluvchilari yoʻq 1 Va lekin , keyin lekin tub son, aks holda lekin kompozit son deb ataladi. Eng katta musbat bo'luvchi d ikkita raqam a Va m eng katta umumiy bo'luvchi (GCD) deb ataladi va belgilang d = (a, m). Agar GCD (a,m)=1 , keyin a Va m dan boshqa umumiy boʻluvchilar yoʻq 1 , va bir-biriga nisbatan koʻp boʻlgan deyiladi.

Har biriga CHEKIRISH da r = 0, 1, 2,…, m-1 butun sonlar to'plamiga mos keladi a, b, ... Ularning aytishicha, raqamlar bir xil CHEKIRISH moduli bilan solishtirish mumkin va b(mod m) yoki (a b) m bilan belgilanadi.

Masalan, qachon m = 3 :

Masalan, qachon m = 5 :

Raqamlar lekin , ular taqqoslanadigan modullardir m , ularning sinfini tashkil qiladi CHEKIRISH r va sifatida belgilanadi a = m q + r.

Raqamlar lekin ham chaqiriladi Chegirmalar modul m . Salbiy bo'lmagan Chegirmalar a = r (da q=0 ) intervaldan qiymatlarni olish , eng kam qoldiq modulining to'liq tizimini tashkil qiladi m.

Chegirmalar lekin , intervaldan qiymatlarni olish [-( ,…,( ] , da g'alati m yoki intervaldan [- da hatto m mutlaq eng kichikning to'liq tizimini hosil qiladi CHEKIRISH s moduli m.

Masalan, qachon m = Eng kam qoldiqlarning 5 klassi hosil bo'ladi

r = 0, 1, 2, 3, 4, a = -2, -1, 0, 1, 2. Berilgan ikkala son toʻplami ham toʻliq sistemalarni hosil qiladi. chegirma s moduli 5 .

Sinf Chegirmalar, uning elementlari modul bilan mos keladi m

qisqartirilgan deb ataladi. Eyler funktsiyasi qanchaligini aniqlaydi Chegirmalar eng kam qoldiq modulining to'liq tizimidan m bilan engish m . Bo'sh turganda m=p bizda = p-1.

Ta'rif. Juftlik bilan taqqoslanmaydigan modullarning maksimal to'plami m raqamlar bilan mos keladi m , deyiladi chegirmalarning qisqartirilgan tizimi modul m. Har qanday kamaytirilgan qoldiqlar tizimi moduli m elementlarni o'z ichiga oladi, bu erda Eyler funktsiyasi.

Ta'rif. Ekvivalentlik sinfidan istalgan raqam qm qo'ng'iroq qilamiz chegirma ohm moduli m. Agregat chegirma s, har bir ekvivalentlik sinfidan bittadan olingan qm, to'liq tizim deb ataladi chegirma s moduli m(to'liq tizimda chegirma ov, shuning uchun jami m raqamlar bo'laklari). To'g'ridan-to'g'ri bo'linganda qoldiqlarning o'zlari m eng kam salbiy deb ataladi chegirma ami va, albatta, to'liq tizimni tashkil qiladi chegirma s moduli m. Chegirma Agar ïrï modullar ichida eng kichigi bo'lsa, r mutlaqo eng kichik deyiladi chegirma bu sinfning s.

Misol. 13, 8, - 3, 10, 35, 60 raqamlari m=6 modulli qoldiqlarning toʻliq sistemasini tashkil etishini tekshiring.

Yechim: Ta'rifga ko'ra, raqamlar modulli qoldiqlarning to'liq tizimini tashkil qiladi m, agar ular aniq m bo'lsa va ular juftlik bilan solishtirib bo'lmaydigan modul bo'lsa m.

Har bir raqamni eng kichik manfiy bo'lmagan qoldiq bilan almashtirish orqali juftlik bilan taqqoslanmasligini tekshirish mumkin; agar takrorlashlar bo'lmasa, demak, bu chegirmalarning to'liq tizimidir.

Qoldiq bilan bo'linish teoremasini qo'llaymiz: a = m q + r.

13 = 6 2 + 1 13 1 (mod 6); 8 = 6 1 + 2 8 2 (mod 6);

3 = 6 (-1) + 3 -3 3 (mod 6); 10 = 6 1 + 4 10 4(mod 6);

35 = 6 5 + 5 35 5 (mod 6); 60 = 6 10 + 0 60 0 (mod 6).

Biz raqamlar ketma-ketligini oldik: 1, 2, 3, 4, 5, 0, ularning aniq 6 tasi bor, hech qanday takrorlash yo'q va ular juftlik bilan taqqoslanmaydi. Ya'ni, ular m = 6 modulli qoldiqlarning to'liq tizimini tashkil qiladi.

Misol. Eng kichik mutlaq qiymat, shuningdek, eng kichik musbat qoldiq 185 modul 16 bilan almashtiring.

Yechim. Qoldiq bilan bo'linish teoremasini qo'llaymiz:

185 = 16 11 + 9 185 9 (mod 16).

Misol. Raqamlar mavjudligini tekshiring (13, -13, 29, -9) qoldiqlarning qisqartirilgan tizimi moduli m=10.

Yechim: Modulli qoldiqlarning har qanday qisqartirilgan tizimi m elementlarni o'z ichiga oladi, bu erda Eyler funktsiyasi. Bizning holatda =4, chunki natural sonlar ichida faqat 1, 3, 7, 9 lar 10 ga nisbatan tub va undan oshmaydi. Ya'ni, bu to'rtta raqam kerakli tizimni tashkil qilishi mumkin. Keling, bu sonlarni juftlik taqqoslanmasligini tekshirib ko'ramiz: =4, chunki natural sonlar ichida faqat 1, 3, 7, 9 lar 10 ga nisbatan tub va undan oshmaydi. Ya'ni, bu to'rtta raqam kerakli tizimni tashkil qilishi mumkin. Keling, bu raqamlarni juftlik bilan taqqoslanmasligini tekshiramiz: m .

Variant 1. a= 185, m = 12; Variant 2. a = 84, m = 9;

Variant 3. a= 180, m = 10; Variant 4. a = 82, m = 9;

Variant 5. a= 85, m = 11; Variant 6. a = 84, m = 8;

Variant 7. a= 103, m = 87; Variant 8. a = 84, m = 16;

Variant 9. a= 15, m = 10; Variant 10. a = 81, m = 9;

Variant 11. a= 85, m = 15; Variant 12. a = 74, m = 13;

Variant 13. a= 185, m = 16; Variant 14. a = 14, m = 9;

Variant 15. a= 100, m = 11; Variant 16. a = 484, m = 15;

Variant 17. a= 153, m = 61; Variant 18. a = 217, m = 19;

Variant 19. a= 625, m = 25; Variant 20. a = 624, m = 25;

3-topshiriq. Eng kamning to`liq va kichraytirilgan tizimini yozing

17-modda. Chegirmalarning to'liq va qisqartirilgan tizimlari.

Oldingi bandda bu nisbat qayd etilgan edi qm solishtirish moduli m butun sonlar to‘plamidagi ekvivalentlik munosabati. Ushbu ekvivalentlik munosabati butun sonlar to'plamining ekvivalent elementlar sinflariga bo'linishini keltirib chiqaradi, ya'ni. raqamlar bir sinfga birlashtirilib, bo'linganda beriladi m bir xil qoldiqlar. Ekvivalentlik sinflari soni qm(mutaxassislar aytadilar - "ekvivalentlik indeksi qm") ga aynan teng m .

Ta'rif. Ekvivalentlik sinfidan istalgan raqam qm qoldiq moduli deb ataladi m. Har bir ekvivalentlik sinfidan bittadan olingan qoldiqlar to'plami qm, qoldiqlar modulining to'liq tizimi deyiladi m(chegirmalarning to'liq tizimida, shuning uchun jami m raqamlar bo'laklari). To'g'ridan-to'g'ri bo'linganda qoldiqlarning o'zlari m eng kam manfiy bo'lmagan qoldiqlar deb ataladi va, albatta, modulli qoldiqlarning to'liq tizimini tashkil qiladi. m. Agar berilgan sinfning qoldiq modullari orasida rp eng kichik bo'lsa, qoldiq r mutlaqo eng kichik deyiladi.

Misol: Bo'lsin m= 5. Keyin:

0, 1, 2, 3, 4 - eng kichik manfiy bo'lmagan qoldiqlar;

2, -1, 0, 1, 2 mutlaqo eng kichik qoldiqlardir.

Ikkala qisqartirilgan raqamlar to'plami modulli qoldiqlarning to'liq tizimini tashkil qiladi 5 .

Lemma 1. 1) Har qanday m modul bo'yicha taqqoslanmaydigan juft bo'laklar m raqamlar modulli qoldiqlarning to'liq tizimini tashkil qiladi m .

2) Agar lekin Va m ko'p sonli, va xm, keyin chiziqli shaklning qiymatlari ax+b, qayerda b- har qanday butun son, shuningdek, modulli qoldiqlarning to'liq tizimidan o'tadi m .

Isbot. Tasdiqlash 1) aniq. Keling, 2 ta fikrni isbotlaylik). Raqamlar ax+b silliq m narsalar. Keling, ularni bir-biri bilan modul bilan solishtirish mumkin emasligini ko'rsataylik m. Xo'sh, biroz boshqacha bo'lsin x 1 Va x2 chegirmalarning to'liq tizimidan ma'lum bo'ldi ax 1 +b ê ax 2 +b(mod m). Keyin, oldingi paragrafdagi taqqoslash xususiyatlariga ko'ra, biz quyidagilarni olamiz:

ax 1 - bolta 2 (mod m)

x 1 x 2 (mod m)

- nima bilan ziddiyat x 1 Va x2 farqlanadi va ajratmalarning to‘liq tizimidan olinadi.

Berilgan ekvivalentlik sinfidagi barcha raqamlar ê ga karrali sonni qo'shish orqali berilgan sinfning bir raqamidan olinadi. m, keyin bu sinfdagi barcha raqamlar modulga ega m bir xil eng katta umumiy bo'luvchi. Ba'zi sabablarga ko'ra, modul bilan bo'lgan ajratmalar m birga teng eng katta umumiy bo'luvchi, ya'ni. modulga nisbatan asosiy bo'lgan qoldiqlar.

Ta'rif. Modulli qoldiqlarning qisqartirilgan tizimi m to'liq tizimning modulga mos keladigan barcha qoldiqlari to'plamidir m .

Qisqartirilgan tizim odatda eng kichik salbiy bo'lmagan qoldiqlardan tanlanadi. Ko'rinib turibdiki, qoldiqlar moduli kamayadi m j o'z ichiga oladi ( m) qoldiq bo'laklari, bu erda j ( m) Eyler funksiyasi, dan kichik sonlar soni m va bilan tenglashing m. Agar shu paytgacha siz Eyler funksiyasini unutgan boʻlsangiz, 14-bandga qarang va u yerda bu haqda biror narsa aytilganligiga ishonch hosil qiling.

Misol. Bo'lsin m= 42. U holda qoldiqlarning qisqartirilgan tizimi:

1, 5, 11, 13, 17, 19, 23, 25, 29, 31, 37, 41.

Lemma 2. 1) har qanday j ( m) juftlik bilan solishtirib bo'lmaydigan modulli sonlar m va modulga nisbatan tub bo'lib, modulli qoldiqlarning qisqartirilgan tizimini hosil qiladi m .

2) Agar (a, m) = 1 Va x qoldiq modulining qisqartirilgan tizimi orqali ishlaydi m, keyin bolta qoldiq modulining qisqartirilgan tizimi orqali ham ishlaydi m .

Isbot. Tasdiqlash 1) aniq. Keling, 2 ta fikrni isbotlaylik). Raqamlar bolta juftlik bilan solishtirib bo'lmaydi (bu xuddi shu kichik bo'limning 1-Lemmasida bo'lgani kabi isbotlangan), aynan j ( m) narsalar. Bundan tashqari, ularning barchasi modulga nisbatan asosiy ekanligi aniq, chunki (a,m)=1, (x,m)=1 X (ax.m)=1. Shunday qilib, raqamlar bolta chegirmalarning qisqartirilgan tizimini tashkil qiladi.

Bu qoldiqlarning to'liq va qisqartirilgan tizimlarining ta'riflari va asosiy xususiyatlari, ammo matematik bilimlar bagajida qoldiqlar tizimlariga oid bir qator juda qiziqarli va foydali faktlar hali ham mavjud. Agar biz ushbu bandda ular haqida sukut saqlasak, men qo'rqamanki, bu Rossiya Federatsiyasining Axborot to'g'risidagi qonunini to'g'ridan-to'g'ri buzish bo'ladi, bu qonunga ko'ra g'arazli yashirish ma'muriy va hatto jinoiy javobgarlikka tortiladi. harakat. Bundan tashqari, chegirma tizimlarining boshqa muhim xususiyatlari bilan tanishmasdan, 17-band juda qisqa bo'lib chiqadi. Davom etaylik.

Lemma 3. Bo'lsin m 1, m 2, ..., m k juft koʻlamli va m 1 m 2 ...m k =M 1 m 1 =M 2 m 2 =...=M k m k, qayerda

1) Agar x 1 , x 2 , ..., x k modulli qoldiqlarning to'liq tizimlari orqali ishlaydi m 1, m 2, ..., m k qoldiq modulining to'liq tizimidan o'ting m=m 1 m 2 ...m k .

2) Agar x 1 , x 2 , ..., x k qoldiq modullarining qisqartirilgan tizimlaridan o'ting m 1, m 2, ..., m k mos ravishda, keyin chiziqli shaklning qiymatlari qoldiq modulining qisqartirilgan tizimidan o'ting m=m 1 m 2 ...m k .

Isbot.

1) Shakl M 1 x 1 +M 2 x 2 + ...+M k x k olishi aniq m 1 m 2 ...m k =m qiymatlar. Keling, ushbu qiymatlarni juftlik bilan taqqoslab bo'lmasligini ko'rsataylik. Mayli, ruxsat bering

M 1 x 1 +M 2 x 2 + ...+M k x kê M 1 x 1 C +M 2 x 2 C + ...+M k x k C (mod m)

Har qanday narsa Mj, dan farqli Xonim, bir nechta Xonim. Oxirgi taqqoslashda chap va o'ng shartlarni olib tashlash, ko'paytmalari Xonim, biz olamiz:

M s x s ê M s x s C (mod m s) Yu x sê x s C (mod m s)

- nima bilan ziddiyat x s qoldiq modulining to'liq tizimidan o'tadi Xonim .

2). Shakl M 1 x 1 +M 2 x 2 + ...+M k x k aniq j oladi ( m 1) j ( m2) Ch ... Ch j ( m k) = j( m 1 m 2 Vt ... Vt m k)= j ( m) (Eyler funktsiyasi multiplikativdir!) turli qiymatlar, qaysi modul m=m 1 m 2 ...m k juftlik bilan taqqoslanmaydi. Ikkinchisi, ushbu lemmaning 1) tasdig'ini isbotlashda ishlatiladigan dalillarga o'xshash dalillar bilan osongina isbotlanadi. Chunki ( M 1 x 1 +M 2 x 2 + ...+M k x k ,m s)=(M s x s ,m s)=1 har biriga 1 J s J k, keyin ( M 1 x 1 +M 2 x 2 + ...+M k x k ,m s)=1, shuning uchun shakl qiymatlari to'plami M 1 x 1 +M 2 x 2 + ...+M k x k qoldiq modulining qisqartirilgan tizimini hosil qiladi m .

Lemma 4. Bo'lsin x 1 , x 2 , ..., xk ,x to'liq yugurish, va x 1 , x 2 ,..., x k , x- modullardagi qoldiqlarning qisqartirilgan tizimlaridan o'tish m 1, m 2, ..., m k Va m=m 1 m 2 ...m k mos ravishda, qaerda (m i m j)=1 da i № j. Keyin kasrlar kasrlar bilan mos (x/m), va kasrlar kasrlar bilan mos (x/m) .

Isbot. Lemma 4 ga oid ikkala tasdiqning isbotini har bir summani berganingizdan keyin oldingi Lemma 3 ni qo'llash orqali osongina olish mumkin. (x 1 /m 1 +x 2 /m 2 +...+x k /m k) Va ( x 1 /m 1 + x 2 /m 2 +...+ x k /m k) umumiy maxrajga:

(x 1 /m 1 +x 2 /m 2 +...+x k /m k )=((M 1 x 1 +M 2 x 2 +...+M k x k)/m) ;

( x 1 /m 1 + x 2 /m 2 +...+ x k /m k )=((M 1 x 1 +M 2 x 2 +...+M k x k)/m) ,

qayerda M j =m 1 ...m j-1 m j+1 ...m k .

Endi hisobga oladigan bo'lsak, sonlarning kasr qismlari modulga bo'linish yo'li bilan olinadi m modul bo'yicha taqqoslanadigan har qanday ikkita raqam m, bir xil (ular teng r/m, qayerda r berilgan sinfdan eng kichik manfiy bo'lmagan qoldiq), keyin hozirgi lemmaning tasdiqlari aniq bo'ladi.

Ushbu bo'limning qolgan qismida eng qiziqarli narsa bo'ladi - biz murakkab ildizlarni jamlaymiz m th kuchini birlikdan oladi va biz ildiz yig'indilari, qoldiq tizimlari va allaqachon tanish bo'lgan multiplikativ Möbius funktsiyasi m ( m) .

e k bilan belgilang k- ildiz m- oh birlik darajasi:

Kompleks sonlarni yozishning bu shakllarini birinchi yildan yaxshi eslaymiz. Bu yerda k=0,1,...,m-1– qoldiq modullarining to‘liq tizimidan o‘tadi m .

Eslatib o'tamiz, miqdor e 0 + e 1 +...+ e m-1 barcha ildizlar m birlik kuchi har qanday uchun nolga teng m. Haqiqatan ham, ruxsat bering e 0 + e 1 +...+ e m-1 =a. Keling, bu summani nolga teng bo'lmagan e 1 raqamiga ko'paytiramiz. Murakkab tekislikda geometrik tarzda bunday ko'paytirish to'g'ri aylanishni anglatadi m-gon, uning uchlarida ildizlari joylashgan e 0 , e 1 ,..., e m-1, nolga teng bo'lmagan burchakka 2p/m. Bu holda ildiz bo'lishi aniq e 0 ildizga o'ting e 1, ildiz e 1 ildizga o'ting e 2 va boshqalar va ildiz e m-1 ildizga o'ting e 0, ya'ni. so'm e 0 + e 1 +...+ e m-1 O'zgarmaydi. Bizda ... bor e 1 a=a, qayerda a=0 .

Teorema 1. Bo'lsin m>0- butun son, a O Z , x qoldiq modulining to'liq tizimidan o'tadi m. Keyin agar lekin bir nechta m, keyin

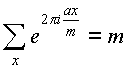
aks holda, qachon lekin ko'p emas m ,

.

Isbot. Da lekin bir nechta m bizda ... bor: a=md Va

Da lekin ga bo'linmaydi m, kasrning soni va maxrajini ajrating a/m ustida d eng katta umumiy boʻluvchidir lekin Va m, biz kamaytirilmaydigan kasrni olamiz a 1 / m 1. Keyin, Lemma 1 tomonidan, a 1 x qoldiq modulining to'liq tizimidan o'tadi m. Bizda ... bor:

chunki darajaning barcha ildizlarining yig'indisi m 1 birlikdan nolga teng.

Ildiz ekanligini unutmang e k m Agar uning indeksi bo'lsa, birlik kuchi antiderivativ deb ataladi k bilan o'zaro oddiy m. Bu holda, birinchi yilda isbotlanganidek, ketma-ket darajalar e k 1 , e k 2 ,..., e k m-1 ildiz e k ildizlarning butun majmuasini hosil qiladi m kuch birlikdan yoki boshqacha qilib aytganda, e k barcha ildizlarning siklik guruhining generatoridir m birlikdan th daraja.

Shubhasiz, turli xil ibtidoiy ildizlarning soni m birlik kuchi j ga teng ( m), bu erda j - Eyler funktsiyasi, chunki ibtidoiy ildizlarning indekslari modulli qoldiqlarning qisqartirilgan tizimini tashkil qiladi. m .

Teorema 2. Bo'lsin m>0 butun son bo'lib, x qoldiq modulining qisqartirilgan tizimidan o'tadi m. Keyin (darajaning ibtidoiy ildizlari yig'indisi m):

qayerda m ( m) Möbius funktsiyasidir.

Isbot. Bo'lsin m=p 1 a 1 p 2 a 2 ...p k a k sonning kanonik kengayishi hisoblanadi m ; m 1 \u003d p 1 a 1 , m 2 \u003d p 2 a 2 , m 3 \u003d p 3 a 3; x i modulli qoldiqlarning qisqartirilgan tizimidan o'tadi m i. Bizda ... bor:

Da a s =1 faqat ildiz ekanligi ma'lum bo'ldi e 0 =1 ibtidoiy emas, shuning uchun barcha ibtidoiy ildizlarning yig'indisi barcha ildizlarning yig'indisi minus bitta:

shuning uchun agar m kvadratlardan ozod (ya'ni bo'linmaydi r2, da r>1), keyin

Agar biron bir ko'rsatkich bo'lsa a s birdan kattaroq (masalan, m tomonidan bo'linadi r2, da r>1), keyin darajaning barcha ibtidoiy ildizlari yig'indisi Xonim darajaning barcha ildizlarining yig'indisidir Xonim minus barcha ibtidoiy bo'lmagan ildizlarning yig'indisi, ya'ni. barcha ildizlar ma'lum darajada kamroq Xonim. Aynan, agar m s =p s m s *, keyin:

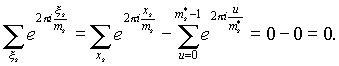
Endi, aziz o'quvchilar, men sizning e'tiboringizga to'liq va qisqartirilgan chegirma tizimlari to'g'risida juda katta miqdordagi ma'lumotlarni taqdim etganimda, hech kim meni Rossiya Federatsiyasining Axborot to'g'risidagi qonunini qasddan buzganlikda ayblay olmaydi, shuning uchun men buni tugataman. mamnuniyat bilan paragraf.

boshqotirmalar

1 . Bir qog'oz varag'iga barcha eng kichik manfiy bo'lmagan qoldiqlarni va barcha mutlaqo eng kichik qoldiqlarni yozing. a) modul 6, b) modul 8. Quyida ushbu modullar uchun berilgan chegirma tizimlarini yozing. Murakkab tekislikda birlikning oltinchi va sakkizinchi ildizlarining ildizlarini alohida chizing, ikkala raqamda ibtidoiy ildizlarni aylantiring va har bir holatda ularning yig'indisini toping. 2 . Bo'lsin e- ibtidoiy ildiz 2n birlikdan. Miqdorni toping: 1+ e + e 2 +...+ e n-1 . 3 . Barcha tub ildizlarning yig‘indisini toping: a) 15-; b) 24; c) birlikdan 30-darajali. 4 . Ibtidoiy ildizlarning barcha mumkin bo‘lgan hosilalari yig‘indisini toping n birdan th daraja, ikkitadan olingan. 5 . summasini toping k-barcha ildizlarning x kuchi n birlikdan th daraja. 6 . Bo'lsin m>1 , (a, m)=1 , b butun son, X to'liq bo'ylab ishlaydi va x qoldiq modulining qisqartirilgan tizimidan o'tadi m. Buni isbotlang: lekin) b) 7 . Buni isbotlang: , qayerda R sonning barcha tub bo‘luvchilari orqali o‘tadi lekin .

To'liq hisob-kitob tizimi. Berilgan chegirmalar tizimi. Eng keng tarqalgan chegirma tizimlari: eng kam ijobiy, eng kam salbiy, mutlaqo eng kam va boshqalar.

Teorema 1. To'liq va qisqartirilgan qoldiqlar tizimining xususiyatlari.

1°.Chigirmalarning to'liq tizimi mezonlari. Har qanday kombinatsiya m juftlik bilan taqqoslanmaydigan modul bo'lgan butun sonlar m, qoldiqlar modulining to'liq tizimini tashkil qiladi m.

2°. Agar raqamlar x 1 , x 2 , ..., x m- modulli qoldiqlarning to'liq tizimi m, (a, m) = 1, b ixtiyoriy butun son, keyin raqamlar bolta 1 +b, bolta 2 +b, ..., bolta m+b shuningdek, qoldiq modullarining to'liq tizimini tashkil qiladi m.

3°. Qisqartirilgan qisqartirish tizimining mezoni. j( dan tashkil topgan har qanday to'plam m) juftlik bilan taqqoslanmaydigan modul bo'lgan butun sonlar m va modul bilan ko'paytiriladi, modulli qoldiqlarning qisqartirilgan tizimini hosil qiladi m.

4°. Agar raqamlar x 1 , x 2 , ..., x j ( m) - modulli qoldiqlarning qisqartirilgan tizimi m, (a, m) = 1, keyin raqamlar bolta 1 , bolta 2 , ..., a x j ( m) shuningdek, modulli qoldiqlarning qisqartirilgan tizimini tashkil qiladi m.

Teorema 2. Eyler teoremasi.

Agar raqamlar a Va m keyin ko'paytiring a j ( m) º 1 (mod m).

Natija.

1°. Ferma teoremasi. Agar p tub son va a ga bo'linmaydi p, keyin a p–1 º 1 (mod p).

2°. Umumlashtirilgan Ferma teoremasi. Agar p u tub sondir a p º a(mod p) har qanday uchun aÎ Z .

§ 4. O'zgaruvchi bilan taqqoslashlarni yechish

Taqqoslash qarori. Ekvivalentlik. Taqqoslash darajasi.

Teorema. Kongruenslar yechimlarining xossalari.

1°.Kongruentlarning yechimlari qoldiqlarning butun sinflaridir.

2°. (" k)(a k º b k(mod m))Ù k= taqqoslashning z º 0 (mod m) va º 0 (mod m) ekvivalentdir.

3°. Agar taqqoslashning ikkala qismi modul bilan ko'paytiriladigan songa ko'paytirilsa, u holda asl nusxaga ekvivalent bo'lgan taqqoslash olinadi.

4°. Har qanday taqqoslash moduli asosiy p darajasi oshmaydigan taqqoslashga teng p–1.

5°. Taqqoslash º 0 (mod p), qayerda p tub son bo‘lib, ko‘pi bilan ega n turli yechimlar.

6°. Vilson teoremasi. ( n-bir)! º –1 (mod n) Û n Bosh raqam.

§ besh. Birinchi darajali taqqoslashlarni yechish

bolta º b(mod m).

Teorema. 1°. Agar ( a, m) = 1, u holda taqqoslashning yechimi bor va u yagonadir.

2°. Agar ( a, m) = d Va b ga bo'linmaydi d, keyin taqqoslash hech qanday yechimga ega emas.

3°. Agar ( a, m) = d Va b tomonidan bo'linadi d, keyin taqqoslash mavjud d modul qoldiqlarining bir sinfini tashkil etuvchi turli yechimlar.

Taqqoslashlarni yechish usullari bolta º b(mod m) qachon ( a, m) = 1:

1) tanlash (chegirmalarning to'liq tizimining elementlarini sanab o'tish);

2) Eyler teoremasidan foydalanish;

3) Evklid algoritmidan foydalanish;

4) koeffitsientlarni o'zgartirish (2.2-teoremadagi qoldiqlarning to'liq tizimining 2 ° xususiyatidan foydalangan holda);

§6. Birinchi darajali noaniq tenglamalar

bolta+tomonidan = c.

Teorema. Tenglama bolta+tomonidan = c echilishi mumkin bo'lgan taqdirda c (a, b).

Qachon ( a, b) = 1 tenglamaning barcha yechimlari formulalar bilan berilgan

tÎ Z , qayerda x 0 ba'zi taqqoslash echimidir

bolta º c(mod b), y 0 = .

Diofant tenglamalari.

10-BOB. Murakkab sonlar

Kompleks sonlar sistemasiga ta'rif. Kompleks sonlar sistemasining mavjudligi

Kompleks sonlar sistemasiga ta'rif.

Teorema. Kompleks sonlar tizimi mavjud.

Model: R 2 operatsiyalar bilan

(a, b)+(c, d) = (a+c, b+d), (a, b)×( c, d) = (ac–bd, mil. avv+e'lon),

i= (0, 1) va identifikatsiya lekin = (lekin, 0).

Kompleks sonning algebraik shakli

Kompleks sonning shaklda ifodalanishi z = a+bi, qayerda a, bÎ R , i 2 = -1. Bunday vakillikning o'ziga xosligi. Re z, Im z.

Kompleks sonlar ustida arifmetik amallarni algebraik shaklda bajarish qoidalari.

Arifmetika n-o'lchovli vektor fazosi C n. Chiziqli tenglamalar, matritsalar va determinantlar tizimi C .

Kompleks sonlardan kvadrat ildizlarni algebraik shaklda ajratib olish.
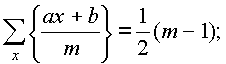