Skaičių rinkinys, palyginamas su a modulo m paskambino skaičių klasė modulo m(arba lygiavertiškumo klasė). Visi tos pačios klasės skaičiai turi formą mt+ r fiksuotame r.

Už duotybę m, r gali gauti reikšmes nuo 0 iki m-1, t.y. viskas egzistuoja m skaičių klasės modulo m, o bet kuris sveikasis skaičius pateks į vieną iš modulo klasių m. Šiuo būdu,

Z= m m … [m-1]m, kur [ r]m={x Z: x≡r(mod m)}

Bet koks klasės skaičius [ r]m paskambino minusas modulo m visų tos pačios klasės skaičių atžvilgiu. Skaičius, lygus likusiai daliai r, vadinamas mažiausias neneigiamas likutis.

Mažiausios absoliučios vertės liekana vadinama absoliučiai mažiausiai atskaitoma.

Pavyzdys

Paimkime modulį m=5. Paleisk a=8. Pasiskirstykime a ant m su likusia dalimi:

Priminimas r=3. Taigi 8 5 , o mažiausia neneigiama 8 modulio 5 liekana yra 3.

Absoliučiai mažiausią likutį galima rasti apskaičiavus r-m=3-5=-2 ir palyginus absoliučias reikšmes|-2| ir |3|. |-2|<|3|, значит -2 – абсолютно наименьший вычет числа 8 по модулю 5.

Iš kiekvienos klasės paėmę vieną išskaitymą, gauname pilna atsiskaitymo sistema modulo m. Jei visi šie skaičiai yra mažiausi neneigiami likučiai modulo m, tada tokia likučių sistema vadinama pilna mažiausiai neneigiamų likučių sistema, ir žymimas Z m.

{0; 1;…; m-1) = Z m yra visa mažiausiai neneigiamų likučių sistema.

(– ;…; 0;…; ) (jei m-nelyginis skaičius) ;

( - ,…,-1, 0, 1,…, ) arba (- ,…, -1, 0, 1,…, ) (jei m lyginis skaičius) yra visa absoliučiai mažiausiai likučių sistema.

Pavyzdys

Jeigu m=11, tada visa mažiausiai neneigiamų likučių sistema yra (0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10), o visa absoliučiai mažiausiai likučių sistema yra (-5 ; -4; -3; -2; -1; 0; 1; 2; 3; 4; 5).

1 teiginys

Bet koks m skaičiai, kurie yra nepalyginami poromis modulo m, sudaro visą likučių sistemą modulo this.

Įrodymas:

Iš tiesų, dėl nepalyginamumo šie skaičiai priklauso skirtingoms klasėms, ir nuo to laiko juos m vienetų, tada lygiai vienas skaičius patenka į kiekvieną esamą klasę.

2 teiginys

Jei ( a, m) = 1 ir x eina per visą modulo likučių sistemą m, tada kirvis+b, kur b- bet koks skaičius nuo Z, taip pat eina per visą modulio likučių sistemą m.

Įrodymas:

Skaičiai kirvis+b bus tiksliai m dalykų. Belieka įrodyti, kad bet kurie 2 skaičiai kirvis 1 +b Ir kirvis 2 +b neprilygstamas modulis m, jei x 1 x 2 (mod m)

Įrodymas prieštaravimu. Apsimeskime tai kirvis 1 +b≡ kirvis 2 +b(mod m) pagal 4-ąjį Šv. kirvis 1 ≡ kirvis 2 (mod m) remiantis St-va palyginimais Nr. 9 ir tuo, kad ( a, m) = 1, turime x 1 ≡ x 2 (mod m). Turime prieštaravimą tam, kad x 1 x 2 (mod m). Todėl prielaida yra klaidinga, taigi ir atvirkščiai. T.y kirvis 1 +b Ir kirvis 2 +b neprilygstamas modulis m, jei x 1 x 2 (mod m), kas turėjo būti įrodyta.

Ankstesniame skyriuje aptarta padalijimo lygtis () turi du įėjimus (a ir n) ir du išėjimus (q ir r). Modulinėje aritmetikoje mus domina tik vienas iš išėjimų, likusi dalis r. Mums nerūpi privatus q . Kitaip tariant, kai dalijame a iš n, mus domina tik kas likučio vertė yra r . Tai reiškia, kad aukščiau pateiktos lygties vaizdą galime pavaizduoti kaip dvejetainis operatorius su dviem įėjimais a ir n ir vienu išėjimu r .

Modulo operacijos

minėtas dvejetainis operatorius pavadintas modulio operatorius ir žymimas kaip mod . Antroji įvestis (n) yra pavadinta modulis. Išvestis r pavadinta minusas. 2.9 paveiksle parodytas padalijimo santykis su modulio operatoriumi.

Ryžiai. 2.9.

Ryžiai. 2.13.

Tiesą sakant, naudojami du operatorių rinkiniai: pirmasis rinkinys yra vienas iš dvejetainiai operatoriai; antrasis – modulo operatoriai. Norėdami pabrėžti darbo tvarką, turime naudoti skliaustus. Kaip parodyta pav. 2.13, įėjimai (a ir b) gali būti Z arba Z n nariai.

2.16 pavyzdys

Vykdykite šiuos teiginius (iš Z n ):

bet. 7 ir 14 pridėjimas prie Z 15

b. Iš 7 atimkite 11 iki Z 13

in. Padauginkite 11 iš 7 iš Z 20

Sprendimas

(14+7) mod 15 -> (21) mod 15 = 6 (7-11) mod 13 -> (-4) mod 13 = 9 (7x11) mod 20 -> (77) mod 20 = 17

2.17 pavyzdys

Atlikite šias operacijas (iš Z n ):

a. 17 ir 27 papildymas Z 14

b. Iš 12 atimkite 43 iki Z 13

c. Padauginkite 123 iš -10 iš Z 19

Sprendimas

Toliau pateikiami du kiekvienos operacijos žingsniai:

(17 + 27) mod 14 -> (44) mod 14 = 2 (12 - 43) mod 13 -> (-31) mod 13 = 8 ((123) x (-10)) mod 19 -> (-1230) ) mod 19 = 5

Savybės

Jau minėjome, kad du įėjimai trims dvejetainiai operatoriai modulo palyginimas gali naudoti duomenis iš Z arba Z n. Šios savybės leidžia mums pirmiausia susieti dvi įvestis su Z n (jei jos gaunamos iš Z), prieš atliekant tris

Išskaičiavimo klasės. Išskaičiavimo sistemos

Trumpa informacija iš teorijos

Naudojant dalybos su liekana teoremą, sveikųjų skaičių aibę galima suskirstyti į keletą klasių. Apsvarstykite pavyzdį. Leisti būti m = 6. Tada turime šešias sveikųjų skaičių aibės skaidinių klases modulo 6:

r = 1;

r = 2;

r = 3;

r = 4;

r = 5;

per kur r reiškia likusią sveikojo skaičiaus dalį, padalytą iš 6.

Prisiminkite padalijimo teoremą su likusia dalimi:

Teorema: Padalinkite skaičių iš skaičiaus , , su likusia dalimi, tada suraskite sveikųjų skaičių porą q Ir r, kad būtų įvykdytos šios sąlygos: .

Tai lengva įrodyti bet kokiems sveikiesiems skaičiams bet o dalyba su liekana galima ir skaičiais q Ir r yra apibrėžti vienareikšmiškai. Mūsų pavyzdyje visa mažiausiai neneigiamų likučių sistema yra aibė (0, 1, 2, 3, 4, 5); visa mažiausiai teigiamų likučių sistema yra aibė (0, 1, 2, 3, 4, 5); pilna mažiausių absoliučių likučių sistema - aibė (-2, -1, 0, 1, 2, 3); redukuota likučių sistema yra aibė (1,5), kadangi ; faktorių rinkinys

Vienas iš aritmetinių operacijų su duotais sveikaisiais skaičiais atlikimo būdų yra pagrįstas paprastais skaičių teorijos principais. Šio metodo idėja yra ta, kad sveikieji skaičiai pateikiami vienoje iš nepozicinių sistemų - liekamųjų klasių sistemoje. Būtent: vietoj operacijų su sveikaisiais skaičiais jie veikia su šių skaičių dalijimo likučiais iš iš anksto pasirinktų pirminių skaičių - moduliai .

Dažniausiai skaičiai pasirinkti iš pirminių skaičių rinkinio.

Leisti būti …, .

Kadangi dalybos teorema su liekana vyksta sveikųjų skaičių žiede, ty kur , tada žiedas Z, pagal apibrėžimą, yra euklido.

Taigi, kaip skaičius, galite pasirinkti likučius iš skaičiaus padalijimo BET ant p i atitinkamai.

Likučių sistema leidžia atlikti aritmetines operacijas su baigtiniu skaičių rinkiniu, neperžengiant jo ribų. Pilna atskaitymų sistema modulo n yra bet koks rinkinys n poromis nepalyginamas modulis n Sveiki skaičiai. Paprastai kaip visa modulio likučių sistema n paimkite mažiausius neneigiamus likučius

Sveikųjų skaičių dalyba a Ir m pasirodo koeficientas q o likusią dalį r , toks

a = m q + r, 0 r m-1. Priminimas r paskambino ATSKAITA omų modulis m.

Pavyzdžiui, už m = 3 ir už m =5 gauname:

a = m q + r, m = 3	a = m q + r, m = 5
0 = 3 + 0	0 = 5 + 0
1 = 3 + 1	1 = 5 + 1
2 = 3 + 2	2 = 5 + 2
3 = 3 + 0	3 = 5 + 3
4 = 3 + 1	4 = 5 + 4
5 = 3 + 2	5 = 5 + 0
6 = 3 + 0	6 = 5 + 1
7 = 3 + 1	7 = 5 + 2

Jei likusioji dalis lygi nuliui ( r=0 ), tada jie taip sako m dalijasi a visas (arba m daugkartinis a ), tai reiškia m a , ir skaičiai q Ir m vadinami dalikliais a . Akivaizdu 1 a Ir a a . Jeigu a neturi kitų daliklių kaip 1 Ir bet , tada bet yra pirminis skaičius, kitu atveju bet vadinamas sudėtiniu skaičiumi. Didžiausias teigiamas daliklis d du skaičiai a Ir m vadinamas didžiausiu bendruoju dalikliu (GCD) ir žymi d = (a, m). Jei GCD (a,m)=1 , tada a Ir m neturi bendrų daliklių, išskyrus 1 , ir sakoma, kad jie yra pagrindiniai vienas kito atžvilgiu.

Kiekvienam ATSKAITA adresu r = 0, 1, 2,…, m-1 atitinka sveikųjų skaičių aibę a, b,... Jie sako, kad skaičiai su tuo pačiu ATSKAITA yra moduliai palyginami ir žymimi a b(mod m) arba (a b) m .

Pavyzdžiui, kada m = 3 :

Pavyzdžiui, kada m = 5 :

Skaičiai bet , kurios yra panašios modulio m , sudaro savo klasę ATSKAITA r ir yra apibrėžiami kaip a = m q + r.

Skaičiai bet taip pat vadinama ATSKAITYMAI modulo m . Neneigiamas ATSKAITYMAI a = r (at q = 0 ) imant vertes iš intervalo , sudaro visą mažiausiai likučių sistemą modulo m.

ATSKAITYMAI bet , imant vertes iš intervalo [-( ,…,( ] , adresu nelyginis m arba iš intervalo [- adresu net m sudaryti pilną absoliučiai mažiausių sistemą ATSKAITA s modulo m.

Pavyzdžiui, kada m = susidaro 5 mažiausiai likučių klasės

r = 0, 1, 2, 3, 4, a = -2, -1, 0, 1, 2. Abi pateiktos skaičių aibės sudaro užbaigtas sistemas atskaita s modulo 5 .

Klasė ATSKAITYMAI, kurio elementai yra kartu su moduliu m

vadinamas sumažintu. Eulerio funkcija nustato, kiek ATSKAITYMAI iš visos mažiausiai likučių sistemos modulo m koprime su m . Kai tuščia eiga m=p mes turime = p-1.

Apibrėžimas. Didžiausias porų nepalyginamų modulių rinkinys m skaičiai koprime su m , vadinamas sumažinta atskaitymų sistema modulo m. Bet kokia sumažinta likučių sistema modulo m yra elementų, kur yra Eulerio funkcija.

Apibrėžimas. Bet koks skaičius iš lygiavertiškumo klasės єm mes paskambinsime atskaita omų modulis m. Suvestinė atskaita s, paimta po vieną iš kiekvienos lygiavertiškumo klasės єm, vadinama visa sistema atskaita s modulo m(visoje sistemoje atskaita ov, taigi iš viso m skaičių gabalėliai). Tiesiogiai patys likučiai, padalyti iš m vadinami mažiausiai neneigiamais atskaita ami ir, žinoma, sudaryti ištisą sistemą atskaita s modulo m. Atskaita r vadinamas absoliučiai mažiausiu, jei ïrï yra mažiausias tarp modulių atskaita s šios klasės.

Pavyzdys. Patikrinkite, ar skaičiai 13, 8, - 3, 10, 35, 60 sudaro visą likučių sistemą modulo m=6.

Sprendimas: Pagal apibrėžimą skaičiai sudaro visą modulio likučių sistemą m, jei jų yra lygiai m ir jie yra poromis nepalyginami modulio m.

Porinį nepalyginamumą galima patikrinti kiekvieną skaičių pakeičiant mažiausia neneigiama liekana; jei pasikartojimų nėra, tai yra pilna išskaičiavimų sistema.

Taikykime dalybos teoremą su liekana: a = m q + r.

13 = 6 2 + 1 13 1 (6 mod.); 8 = 6 1 + 2 8 2 (6 mod.);

3 = 6 (-1) + 3 -3 3 (mod. 6); 10 = 6 1 + 4 10 4 (6 mod.);

35 = 6 5 + 5 35 5 (6 mod.); 60 = 6 10 + 0 60 0 (6 mod.).

Gavome skaičių seką: 1, 2, 3, 4, 5, 0, jų yra lygiai 6, pasikartojimų nėra ir jie poromis nepalyginami. Tai reiškia, kad jie sudaro visą likučių sistemą modulo m = 6.

Pavyzdys. Pakeiskite mažiausia absoliučia verte, taip pat mažiausia teigiama liekana 185 modulo 16.

Sprendimas. Taikykime dalybos teoremą su liekana:

185 = 16 11 + 9 185 9 (16 mod.).

Pavyzdys. Patikrinkite, ar susidaro skaičiai (13, -13, 29, -9) redukuota likučių sistema modulo m=10.

Sprendimas: bet kokia sumažinta likučių sistema modulo m yra elementų, kur yra Eulerio funkcija. Mūsų atveju =4, nes tarp natūraliųjų skaičių tik 1, 3, 7, 9 yra santykinai pirminiai 10 ir jo neviršija. Tai yra, gali būti, kad šie keturi skaičiai sudaro norimą sistemą. Patikrinkime šių skaičių porinį nepalyginamumą: =4, nes tarp natūraliųjų skaičių tik 1, 3, 7, 9 yra santykinai pirminiai 10 ir jo neviršija. Tai yra, gali būti, kad šie keturi skaičiai sudaro norimą sistemą. Patikrinkime šių skaičių porinį nepalyginamumą: m .

1 variantas. a= 185, m = 12; 2 variantas. a = 84, m = 9;

3 variantas. a= 180, m = 10; 4 variantas. a = 82, m = 9;

5 variantas. a= 85, m = 11; 6 variantas. a = 84, m = 8;

7 variantas. a= 103, m = 87; 8 variantas. a = 84, m = 16;

9 variantas. a= 15, m = 10; 10 variantas. a = 81, m = 9;

11 variantas. a= 85, m = 15; 12 variantas. a = 74, m = 13;

13 variantas. a= 185, m = 16; 14 variantas. a = 14, m = 9;

15 variantas. a= 100, m = 11; 16 variantas. a = 484, m = 15;

17 variantas. a= 153, m = 61; 18 variantas. a = 217, m = 19;

19 variantas. a= 625, m = 25; 20 variantas. a = 624, m = 25;

Užduotis 3. Užrašykite pilną ir sumažintą mažiausiai sistemą

17 punktas. Pilnos ir sumažintos atskaitymų sistemos.

Ankstesnėje pastraipoje buvo pažymėta, kad santykis єm palyginamumo modulis m yra sveikųjų skaičių aibės lygiavertiškumo santykis. Šis ekvivalentiškumo santykis indukuoja sveikųjų skaičių aibės padalijimą į lygiaverčių elementų klases, t.y. skaičiai sujungiami į vieną klasę, padalijus iš m tie patys likučiai. Ekvivalentiškumo klasių skaičius єm(ekspertai sakys – „ekvivalentiškumo indeksas єm“) yra lygiai lygus m .

Apibrėžimas. Bet koks skaičius iš lygiavertiškumo klasės єm bus vadinamas likučių moduliu m. Likučių rinkinys, paimtas po vieną iš kiekvienos lygiavertiškumo klasės єm, vadinama visa likučių sistema modulo m(todėl visoje atskaitymų sistemoje iš viso m skaičių gabalėliai). Tiesiogiai patys likučiai, padalyti iš m vadinamos mažiausiai neneigiamomis liekanomis ir, žinoma, sudaro visą modulo likučių sistemą m. Teigiama, kad liekana r yra absoliučiai mažiausia, jei rp yra mažiausia tarp tam tikros klasės liekanų modulių.

Pavyzdys: Leisti būti m= 5. Tada:

0, 1, 2, 3, 4 – mažiausios neneigiamos liekanos;

2, -1, 0, 1, 2 yra absoliučiai mažiausi likučiai.

Abu sumažinti skaičių rinkiniai sudaro užbaigtas likučių modulio sistemas 5 .

1 lema. 1) bet koks m gabalai poromis, moduliu nepalyginami m skaičiai sudaro visą modulo likučių sistemą m .

2) Jei bet Ir m koprime ir xm, tada tiesinės formos reikšmės kirvis+b, kur b- bet koks sveikasis skaičius, taip pat vykdomas per visą modulio likučių sistemą m .

Įrodymas. 1) teiginys yra akivaizdus. Įrodykime 2 teiginį). Skaičiai kirvis+b sklandžiai m dalykų. Parodykime, kad jie nėra palyginami vienas su kitu modulio m. Na tegul kažkam kitaip x 1 Ir x2 iš visos atskaitymų sistemos paaiškėjo, kad ax 1 +b є ax 2 +b (mod m). Tada pagal ankstesnės pastraipos palyginimų savybes gauname:

axe 1 - axe 2 (mod m)

x 1 x 2 (mod. m)

- prieštaravimas su kuo x 1 Ir x2 yra skirtingi ir paimti iš visos atskaitymų sistemos.

Kadangi visi skaičiai iš tam tikros lygiavertiškumo klasės є gaunami iš vieno tam tikros klasės skaičiaus, pridedant skaičių, kuris yra kartotinis m, tada visi šios klasės skaičiai turi modulo m tas pats didžiausias bendras daliklis. Dėl tam tikrų priežasčių tie atskaitymai, kuriuos turi su moduliu m didžiausias bendras daliklis lygus vienetui, t.y. likučiai, kurie yra santykinai aukščiausi modulio atžvilgiu.

Apibrėžimas. Sumažinta likučių sistema modulo m yra visų likučių iš visos sistemos koprime su moduliu rinkinys m .

Redukuota sistema dažniausiai pasirenkama iš mažiausių neneigiamų likučių. Akivaizdu, kad sumažinta likučių sistema modulo m yra j ( m) liekanų gabaliukai, kur j ( m) yra Eulerio funkcija, skaičių, mažesnių nei m ir koprime su m. Jei iki šiol jau pamiršote Eulerio funkciją, pažiūrėkite į 14 pastraipą ir įsitikinkite, kad ten apie ją kažkas buvo pasakyta.

Pavyzdys. Leisti būti m= 42. Tada redukuota likučių sistema yra:

1, 5, 11, 13, 17, 19, 23, 25, 29, 31, 37, 41.

2 lema. 1) bet kuris j ( m) skaičiai, kurie yra nepalyginami poromis modulio m ir santykinai prilyginti moduliui, sudaro redukuotą modulio likučių sistemą m .

2) Jei (a, m) = 1 Ir x eina per sumažintą likučių sistemą modulo m, tada kirvis taip pat eina per sumažintą likučių modulo sistemą m .

Įrodymas. 1) teiginys yra akivaizdus. Įrodykime 2 teiginį). Skaičiai kirvis yra nepalyginami poromis (tai įrodoma taip pat, kaip ir šio poskyrio 1 lemoje), yra lygiai j ( m) dalykus. Taip pat aišku, kad jie visi yra gana svarbūs moduliui, nes (a,m)=1, (x,m)=1 X (ax.m)=1. Taigi skaičiai kirvis sudaryti sumažintą atskaitymų sistemą.

Tai yra pilnų ir sumažintų likučių sistemų apibrėžimai ir pagrindinės savybės, tačiau matematinių žinių bagaže vis dar yra nemažai įdomių ir naudingų faktų apie likučių sistemas. Jei šioje dalyje apie juos nutylime, tai, bijau, bus tiesioginis Rusijos Federacijos informacijos įstatymo pažeidimas, kurio piktybinis slėpimas pagal šį įstatymą yra administracine ir net baudžiama. veikti. Be to, nežinant apie kitas svarbias išskaičiavimo sistemų savybes, 17 punktas pasirodys labai trumpas. Tęskime.

3 lema. Leisti būti m 1, m 2, ..., m k yra porinis koprime ir m 1 m 2 ...m k =M 1 m 1 =M 2 m 2 =...=M k m k, kur

1) Jei x 1 , x 2 , ..., x k paleisti per visas likučių sistemas modulo m 1, m 2, ..., m k paleisti per visą likučių sistemą modulo m=m 1 m 2 ...m k .

2) Jei x 1 , x 2 , ..., x k paleisti per sumažintas likučių sistemas modulo m 1, m 2, ..., m k atitinkamai, tada tiesinės formos reikšmės paleisti per sumažintą likučių sistemą modulo m=m 1 m 2 ...m k .

Įrodymas.

1) Forma M 1 x 1 +M 2 x 2 + ...+M k x k aišku ima m 1 m 2 ...m k =m vertybes. Parodykime, kad šios vertės yra nepalyginamos. Na tegul

M 1 x 1 +M 2 x 2 + ...+M k x k є M 1 x 1 C +M 2 x 2 C + ...+M k x k C (mod m)

bet ko Mj, skiriasi nuo ponia, daugkartinis m s. Paskutiniame palyginime pašalinami kairieji ir dešinieji terminai, kartotiniai m s, mes gauname:

M s x s є M s x s C (mod m s) Yu x s ​​є x s C (mod m s)

- prieštaravimas su kuo x s eina per visą modulo likučių sistemą m s .

2). Forma M 1 x 1 +M 2 x 2 + ...+M k x k akivaizdžiai trunka j ( m 1) j ( m2) Ch... Ch j ( m k) = j( m 1 m 2 W ... W m k)= j ( m) (Eulerio funkcija yra dauginamoji!) skirtingų reikšmių, kurios modulio m=m 1 m 2 ...m k poromis nepalyginami. Pastarasis yra lengvai įrodomas argumentais, panašiais į tuos, kurie naudojami šios lemos 1) tvirtinimo įrodyme. Nes ( M 1 x 1 +M 2 x 2 + ...+M k x k ,m s)=(M s x s, m s)=1 kiekvienam 1 J s J k, tada ( M 1 x 1 +M 2 x 2 + ...+M k x k ,m s) = 1, taigi ir formos verčių rinkinys M 1 x 1 +M 2 x 2 + ...+M k x k formuoja redukuotą likučių sistemą modulo m .

4 lema. Leisti būti x 1 , x 2 , ..., xk , x paleisti pilnas, ir x 1 , x 2 ,..., x k , x– pereiti per sumažintas likučių sistemas moduliuose m 1, m 2, ..., m k Ir m=m 1 m 2 ...m k atitinkamai kur (m i m j) = 1 adresu i № j. Tada trupmenos suderinti su trupmenomis (x/m), ir trupmenomis suderinti su trupmenomis (x/m) .

Įrodymas. Abiejų 4 lemos teiginių įrodymas lengvai gaunamas pritaikius ankstesnę 3 lemą po to, kai pateikiate kiekvieną sumą (x 1 /m 1 +x 2 /m 2 +...+x k /m k ) Ir ( x 1 /m 1 + x 2 /m 2 +...+ x k / m k )į bendrą vardiklį:

(x 1 /m 1 +x 2 /m 2 +...+x k /m k )=((M 1 x 1 +M 2 x 2 +...+M k x k)/m) ;

(x 1 /m 1 + x 2 /m 2 +...+ x k /m k )=((M 1 x 1 +M 2 x 2 +...+M k x k)/m) ,

kur M j =m 1 ...m j-1 m j+1 ...m k .

Jei dabar atsižvelgsime į tai, kad trupmeninės skaičių dalys, gautos padalijus iš modulio m bet kurie du skaičiai, palyginami pagal modulį m, yra vienodi (jie yra lygūs r/m, kur r yra mažiausias neneigiamas likutis iš duotosios klasės), tada dabartinės lemos teiginiai tampa akivaizdūs.

Likusioje šio skyriaus dalyje įvyks įdomiausias dalykas – susumuosime kompleksines šaknis m galia iš vienybės, ir mes atrasime nuostabius ryšius tarp šakninių sumų, likučių sistemų ir jau pažįstamos dauginamosios Möbius funkcijos m ( m) .

Pažymėti e k k– šaknis m- o laipsnis nuo vienybės:

Šias sudėtingų skaičių rašymo formas gerai prisimename nuo pirmųjų metų. čia k=0,1,...,m-1– eina per visą likučių modulo sistemą m .

Prisiminkite, kad suma e 0 + e 1 +...+ e m-1 visos šaknys m vienybės galia yra lygi nuliui bet kuriam m. Tikrai, tegul e 0 + e 1 +...+ e m-1 =a. Padauginkime šią sumą iš nulinio skaičiaus e 1 . Toks geometrinis dauginimas kompleksinėje plokštumoje reiškia teisingo pasukimą m-gon, kurio viršūnėse yra šaknys e 0 , e 1 ,..., e m-1, iki nulinio kampo 2p/m. Akivaizdu, kad šiuo atveju šaknis e 0 eiti į šaknį e 1, šaknis e 1 eiti į šaknį e 2 ir tt, ir šaknis e m-1 eiti į šaknį e 0, t.y. suma e 0 + e 1 +...+ e m-1 Nepakeis. Mes turime e 1 a=a, kur a=0 .

1 teorema. Leisti būti m>0- sveikasis skaičius, a O Z , x eina per visą modulo likučių sistemą m. Tada jei bet daugkartinis m, tada

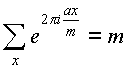
kitu atveju, kada bet ne kartotinis m ,

.

Įrodymas. At bet daugkartinis m mes turime: a=md Ir

At bet nedalomas iš m, padalinkite trupmenos skaitiklį ir vardiklį esu ant d yra didžiausias bendras daliklis bet Ir m, gauname neredukuojamą trupmeną a 1 /m 1. Tada pagal 1 lemą a 1x veiks per visą modulo likučių sistemą m. Mes turime:

nes visų laipsnio šaknų suma m 1 nuo vienybės lygus nuliui.

Atminkite, kad šaknis e k m Vienybės galia vadinama antiderivatine, jei jos indeksas k abipusiai paprasta su m. Šiuo atveju, kaip įrodyta pirmaisiais metais, nuoseklūs laipsniai e k 1, e k 2,..., e k m-1šaknis e k sudaro visą šaknų rinkinį m galia iš vienybės arba, kitaip tariant, e k yra visų šaknų ciklinės grupės generatorius m laipsnis nuo vienybės.

Akivaizdu, kad skirtingų primityvių šaknų skaičius m vienybės galia lygi j ( m), kur j yra Eulerio funkcija, nes primityvių šaknų indeksai sudaro redukuotą likučių sistemą modulo m .

2 teorema. Leisti būti m>0 yra sveikasis skaičius, x eina per sumažintą likučių sistemą modulo m. Tada (primityviųjų laipsnio šaknų suma m):

kur m ( m) yra Möbius funkcija.

Įrodymas. Leisti būti m=p 1 a 1 p 2 a 2 ...p k a k yra kanoninis skaičiaus išplėtimas m ; m 1 \u003d p 1 a 1 , m 2 \u003d p 2 a 2 , m 3 \u003d p 3 a 3; x i eina per sumažintą likučių sistemą modulo m i. Mes turime:

At a s = 1 pasirodo, kad tik šaknis e 0 =1 nėra primityvi, todėl visų primityvių šaknų suma yra visų šaknų suma atėmus vieną:

taigi jei m be kvadratų (t. y. nedalomas iš r2, adresu r>1), tada

Jei koks indikatorius a s didesnis nei vienas (t. y. m padalytą r2, adresu r>1), tada visų primityvių laipsnio šaknų suma m s yra visų laipsnio šaknų suma m s atėmus visų neprimityviųjų šaknų sumą, t.y. visos šaknys tam tikru laipsniu mažiau m s. Būtent, jei m s = p s m s *, tada:

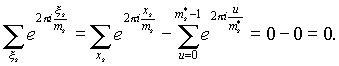
Dabar, gerbiami skaitytojai, kai pateikiau jūsų svarstymui gana nemažą kiekį informacijos apie pilnas ir sumažintas atskaitymo sistemas, niekas negali manęs apkaltinti piktavališku Rusijos Federacijos Informacijos įstatymo pažeidimu jį sulaikant, todėl baigiu tai. pastraipą su pasitenkinimu.

galvosūkiai

1 . Ant popieriaus lapo surašykite visus mažiausius neneigiamus likučius ir visus absoliučiai mažiausius likučius a) modulo 6, b) modulo 8. Tiesiog žemiau užrašykite pateiktas šių modulių atskaitymų sistemas. Atskirai kompleksinėje plokštumoje nubrėžkite šeštos ir aštuntos vienybės šaknis, abiejose figūrose apibraukite primityviąsias šaknis ir kiekvienu atveju raskite jų sumą. 2 . Leisti būti e- primityvi šaknis 2n iš vieneto. Raskite sumą: 1+ e + e 2 +...+ e n-1 . 3 . Raskite visų primityvių šaknų sumą: a) 15-oji; b) 24; c) 30 laipsnis nuo vienybės. 4 . Raskite visų galimų primityvių šaknų sandaugų sumą n laipsnis iš vieno, paimtas dviem. 5 . rasti sumą k-x visų šaknų galios n laipsnis nuo vienybės. 6 . Leisti būti m>1 , (a, m) = 1 , b yra sveikasis skaičius, X eina per visą, o x eina per sumažintą likučių sistemą modulo m. Įrodyk tai: bet) b) 7 . Įrodyk tai: , kur R eina per visus pirminius skaičiaus daliklius bet .

Pilna atsiskaitymo sistema. Pateikta atskaitymų sistema. Labiausiai paplitusios išskaičiavimo sistemos yra šios: mažiausiai teigiamos, mažiausiai neneigiamos, absoliučiai mažiausiai ir kt.

1 teorema. Pilnos ir sumažintos likučių sistemos savybės.

1°.Visos atskaitymų sistemos kriterijai. Bet koks derinys m sveikieji skaičiai, kurie poromis yra nepalyginami modulio m, sudaro pilną likučių sistemą modulo m.

2°. Jei skaičiai x 1 , x 2 , ..., x m– visa modulio likučių sistema m, (a, m) = 1, b yra savavališkas sveikasis skaičius, tada skaičiai kirvis 1 +b, kirvis 2 +b, ..., kirvis m+b taip pat sudaro visą modulo likučių sistemą m.

3°. Sumažinto mažinimo sistemos kriterijus. Bet kuri kolekcija susidedanti iš j( m) sveikieji skaičiai, kurie poromis yra nepalyginami modulio m ir kartu su moduliu sudaro redukuotą modulio likučių sistemą m.

4°. Jei skaičiai x 1 , x 2 , ..., x j ( m) yra sumažinta likučių sistema modulo m, (a, m) = 1, tada skaičiai kirvis 1 , kirvis 2 , ..., a x j ( m) taip pat sudaro sumažintą likučių modulo sistemą m.

2 teorema. Eilerio teorema.

Jei skaičiai a Ir m tada koprime a j ( m) º 1 (mod m).

Pasekmė.

1°. Fermato teorema. Jeigu p yra pirminis skaičius ir a nedalomas iš p, tada a p–1 º 1 (mod p).

2°. Apibendrinta Ferma teorema. Jeigu p tada yra pirminis skaičius a p º a(mod p) bet kuriam aÎ Z .

§ 4. Palyginimų su kintamuoju sprendimas

Palyginimo sprendimas. Lygiavertiškumas. Palyginimo laipsnis.

Teorema. Kongruencijų sprendinių savybės.

1° Kongruencijų tirpalai yra ištisos likučių klasės.

2°. (" k)(a k º b k(mod m))Ù k= z palyginimo º 0 (mod m) ir º 0 (mod m) yra lygiaverčiai.

3°. Jei abi palyginimo dalys padauginamos iš skaičiaus koprime su moduliu, tada gaunamas palyginimas, kuris yra lygiavertis pradiniam.

4°. Bet koks palyginimas modulo a prime p yra lygiavertis palyginimui, kurio laipsnis neviršija p–1.

5°. Palyginimas º 0 (mod p), kur p yra pirminis skaičius, turi daugiausiai nįvairių sprendimų.

6°. Wilsono teorema. ( n- vienas)! º –1 (mod n) Û n Pirminis skaičius.

§ penkta. Pirmojo laipsnio palyginimų sprendimas

kirvis º b(mod m).

Teorema. 1°. Jei ( a, m) = 1, tada palyginimas turi sprendimą ir jis yra unikalus.

2°. Jei ( a, m) = d Ir b nedalomas iš d, tada palyginimas neturi sprendimų.

3°. Jei ( a, m) = d Ir b padalytą d, tada palyginimas turi d skirtingi tirpalai, sudarantys vieną modulio likučių klasę.

Palyginimų sprendimo būdai kirvis º b(mod m) kada ( a, m) = 1:

1) atranka (visos atskaitymų sistemos elementų išvardijimas);

2) Eilerio teoremos panaudojimas;

3) Euklido algoritmo naudojimas;

4) koeficientų kitimas (naudojant visos likučių sistemos savybę 2° iš 2.2 teoremos);

§6. Pirmojo laipsnio neapibrėžtosios lygtys

kirvis+pateikė = c.

Teorema. Lygtis kirvis+pateikė = c galima išspręsti tada ir tik tada c (a, b).

Kada ( a, b) = 1 visi lygties sprendiniai pateikti formulėmis

tÎ Z , kur x 0 yra lyginamasis sprendimas

kirvis º c(mod b), y 0 = .

Diofantinės lygtys.

10 SKYRIUS. Sudėtiniai skaičiai

Kompleksinių skaičių sistemos apibrėžimas. Kompleksinių skaičių sistemos egzistavimas

Kompleksinių skaičių sistemos apibrėžimas.

Teorema. Egzistuoja kompleksinių skaičių sistema.

Modelis: R 2 su operacijomis

(a, b)+(c, d) = (a+c, b+d), (a, b)×( c, d) = (ak–bd, pr. Kr+Reklama),

i= (0, 1) ir identifikavimas bet = (bet, 0).

Algebrinė kompleksinio skaičiaus forma

Kompleksinio skaičiaus vaizdavimas formoje z = a+bi, kur a, bÎ R , i 2 = -1. Tokio vaizdavimo išskirtinumas. Re z, Aš z.

Aritmetinių operacijų su kompleksiniais skaičiais atlikimo algebrine forma taisyklės.

Aritmetika n-dimensinė vektorinė erdvė C n. Tiesinių lygčių, matricų ir determinantų sistemos C .

Kvadratinių šaknų išskyrimas iš kompleksinių skaičių algebrine forma.
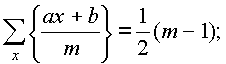