Setul de numere comparabil cu A modulo m numit clasa de numere modulo m(sau o clasă de echivalență). Toate numerele din aceeași clasă au forma mt+ r la un fix r.

Pentru un dat m, r poate lua valori de la 0 la m-1, adică totul există m clase de numere modulo m, iar orice număr întreg se va încadra într-una din clasele modulo m. În acest fel,

Z= m m … [m-1]m, Unde [ r]m={X Z: X≡r(mod m)}

Orice număr de clasă [ r]m numit minus modulo m cu privire la toate numerele din aceeași clasă. Numărul egal cu restul r, se numește cel mai mic reziduu nenegativ.

Se numește reziduul cu cea mai mică valoare absolută absolut cel mai puțin deductibil.

Exemplu

Să luăm modulul m=5. Lăsați-l să plece A=8. Să împărțim A pe m cu restul:

Rest r=3. Deci 8 5 , iar cel mai mic reziduu nenegativ al lui 8 modulo 5 este 3.

Cel mai mic reziduu absolut poate fi găsit calculând r-m=3-5=-2 și comparând valorile absolute ​​|-2| și |3|. |-2|<|3|, значит -2 – абсолютно наименьший вычет числа 8 по модулю 5.

Luând o deducere din fiecare clasă, obținem sistem complet de facturare modulo m. Dacă toate aceste numere sunt cele mai mici reziduuri nenegative modulo m, atunci se numește un astfel de sistem de reziduuri sistem complet de reziduuri cel puțin nenegative, și notat cu Z m.

{0; 1;…; m-1) = Z m este sistemul complet de reziduuri cel puțin nenegative.

(– ;…; 0;…; ) (dacă m-numar impar) ;

(- ,…,-1, 0, 1,…, ) sau (- ,…, -1, 0, 1,…, ) (dacă m număr par) este un sistem complet de reziduuri absolut minime.

Exemplu

În cazul în care un m=11, atunci sistemul complet al celor mai puține reziduuri nenegative este (0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10), iar sistemul complet al celor mai puține reziduuri este (-5 ; -4; -3; -2; -1; 0; 1; 2; 3; 4; 5).

Afirmația 1

Orice m numere care sunt modulo incomparabile perechi m, formează un sistem complet de reziduuri modulo aceasta.

Dovada:

Într-adevăr, din cauza incomparabilității, aceste numere aparțin unor clase diferite și de atunci lor m piese, atunci exact un număr intră în fiecare clasă existentă.

Afirmația 2

În cazul în care un ( A, m) = 1 și X parcurge sistemul complet de reziduuri modulo m, apoi topor+b, Unde b- orice număr de la Z, trece și prin sistemul complet de reziduuri modulo m.

Dovada:

Numerele topor+b va fi exact m lucruri. Rămâne de demonstrat că orice 2 numere topor 1 +bși topor 2 +b modulo incomparabil m, dacă X 1 X 2 (mod m)

Dovada prin contradictie. Să ne prefacem că topor 1 +b≡ topor 2 +b(mod m) in virtutea comparatiilor Sf. 4-va, topor 1 ≡ topor 2 (mod m) în virtutea comparațiilor St-va nr. 9 și a faptului că ( A, m) = 1, avem X 1 ≡ X 2 (mod m). Avem o contradicție cu faptul că X 1 X 2 (mod m). Prin urmare, presupunerea este falsă și, prin urmare, inversul este adevărat. Acesta este topor 1 +bși topor 2 +b modulo incomparabil m, dacă X 1 X 2 (mod m), ceea ce urma să fie dovedit.

Ecuația de împărțire () discutată în secțiunea anterioară are două intrări (a și n) și două ieșiri (q și r). În aritmetica modulară, ne interesează doar una dintre ieșiri, restul r. Nu ne pasă de q privat. Cu alte cuvinte, când împărțim a la n, ne interesează doar ce valoarea restului este r . Aceasta implică faptul că putem reprezenta imaginea ecuației de mai sus ca operator binar cu două intrări a şi n şi o ieşire r .

Operații cu modul

mentionate mai sus operator binar numit operator moduloși este notat ca mod . A doua intrare (n) este numită modul. Ieșirea r este numită minus. Figura 2.9 prezintă relația de divizare față de operatorul modulo.

Orez. 2.9.

Orez. 2.13.

De fapt, se folosesc două seturi de operatori: primul set este unul dintre operatori binari; al doilea este operatori modulo. Trebuie să folosim paranteze pentru a sublinia ordinea lucrării. După cum se arată în fig. 2.13, intrările (a și b) pot fi membri ai lui Z sau Z n .

Exemplul 2.16

Executați următoarele afirmații (care provin de la Z n ):

A. Adăugând 7 și 14 la Z 15

b. Scădeți 11 de la 7 la Z 13

în. Înmulțiți 11 cu 7 în Z 20

Soluţie

(14+7) mod 15 -> (21) mod 15 = 6 (7–11) mod 13 -> (-4) mod 13 = 9 (7x11) mod 20 -> (77) mod 20 = 17

Exemplul 2.17

Efectuați următoarele operații (care provin de la Z n ):

A. Adăugarea 17 și 27 la Z 14

b. Scădeți 43 de la 12 la Z 13

c. Înmulțiți 123 cu -10 în Z 19

Soluţie

Cei doi pași pentru fiecare operație sunt prezentați mai jos:

(17 + 27) mod 14 -> (44) mod 14 = 2 (12 - 43) mod 13 -> (-31) mod 13 = 8 ((123) x (-10)) mod 19 -> (-1230) ) mod 19 = 5

Proprietăți

Am menționat deja că două intrări pentru trei operatori binari compararea modulo poate folosi date de la Z sau Z n . Următoarele proprietăți ne permit să mapăm mai întâi cele două intrări la Z n (dacă provin de la Z ) înainte de a face cele trei

Clase de deducere. Sisteme de deducere

Scurte informații din teorie

Folosind teorema împărțirii cu rest, mulțimea numerelor întregi poate fi împărțită în mai multe clase. Luați în considerare un exemplu. Lăsa m = 6. Atunci avem șase clase de partiții ale mulțimii de întregi modulo 6:

r = 1;

r = 2;

r = 3;

r = 4;

r = 5;

unde prin r denotă restul unui număr întreg împărțit la 6.

Reamintim teorema împărțirii cu rest:

Teorema: Împărțiți un număr la un număr , , cu un rest, apoi găsiți o pereche de numere întregi qși r, astfel încât să fie îndeplinite următoarele condiții: .

Este ușor de demonstrat că pentru orice numere întregi A iar împărțirea cu un rest este posibilă și numere q și r sunt definite fără ambiguitate. În exemplul nostru, sistemul complet al resturilor cel mai puțin nenegative este mulțimea (0, 1, 2, 3, 4, 5); sistemul complet al resturilor cele mai puțin pozitive este mulțimea (0, 1, 2, 3, 4, 5); un sistem complet al celor mai puține reziduuri absolute - o mulțime (-2, -1, 0, 1, 2, 3); sistemul redus de reziduuri este multimea (1,5), deoarece ; set de factori

O metodă de a efectua operații aritmetice pe numere întregi date se bazează pe principii simple ale teoriei numerelor. Ideea acestei metode este că numerele întregi sunt reprezentate într-unul dintre sistemele nepoziționale - în sistemul de clase reziduale. Și anume: în loc de operații pe numere întregi, acestea operează cu resturile împărțirii acestor numere la numere prime preselectate - module .

Cel mai adesea numerele alege dintr-un set de numere prime.

Lăsa …, .

Deoarece teorema împărțirii cu rest are loc în inelul numerelor întregi, adică unde , atunci inelul Z, prin definiție, este euclidiană.

Astfel, ca numere, puteți alege resturile din împărțirea numărului DAR pe p i respectiv.

Sistemul de reziduuri vă permite să efectuați operații aritmetice pe un set finit de numere fără a depăși el. Sistem complet de deduceri modulo n este orice set de n modulo incomparabil pe perechi n numere întregi. De obicei, ca un sistem complet de reziduuri modulo n se iau cele mai mici reziduuri nenegative

Împărțirea numerelor întregi A și m rezultă coeficient q iar restul r , astfel încât

a = m q + r, 0 r m-1. Rest r numit DEDUCERE ohm modulo m.

De exemplu, pentru m = 3 și pentru m =5 obținem:

a = m q + r, m = 3	a = m q + r, m = 5
0 = 3 + 0	0 = 5 + 0
1 = 3 + 1	1 = 5 + 1
2 = 3 + 2	2 = 5 + 2
3 = 3 + 0	3 = 5 + 3
4 = 3 + 1	4 = 5 + 4
5 = 3 + 2	5 = 5 + 0
6 = 3 + 0	6 = 5 + 1
7 = 3 + 1	7 = 5 + 2

Dacă restul este zero ( r=0 ), apoi spun asta m desparte A întreg (sau m multiplu A ), care înseamnă m A , și numerele q și m se numesc divizori A . Evident 1 A și A A . În cazul în care un A nu are alti divizori decat 1 și A , apoi A este un număr prim, în caz contrar A numit număr compus. Cel mai mare divizor pozitiv d doua numere A și m numit cel mai mare divizor comun (MCD) și denotă d = (a, m). Dacă GCD (a,m)=1 , apoi A și m nu au divizori comuni alții decât 1 , și se spune că sunt coprime unul față de celălalt.

Pentru fiecare DEDUCERE la r = 0, 1, 2,…, m-1 corespunde unui set de numere întregi a, b,... Ei spun că numerele cu aceleași DEDUCERE sunt comparabile modulo și sunt notate cu a b(mod m) sau (a b) m .

De exemplu, când m = 3 :

De exemplu, când m = 5 :

Numerele A , care sunt comparabile modulo m , formează o clasă a lor DEDUCERE r și sunt definite ca a = m q + r.

Numerele A numit si DEDUCERI modulo m . Nenegativ DEDUCERI a = r (la q=0 ) preluând valori din interval , formează un sistem complet de cele mai mici reziduuri modulo m.

DEDUCERI A , luând valori din interval [-( ,…,( ] , la ciudat m sau din interval [- la chiar m formează un sistem complet de absolut cel mai mic DEDUCERE s modulo m.

De exemplu, când m = se formează 5 clase de minim reziduuri

r = 0, 1, 2, 3, 4, a = -2, -1, 0, 1, 2. Ambele seturi date de numere formează sisteme complete deducere s modulo 5 .

Clasă DEDUCERI, ale căror elemente sunt coprime cu modulul m

se numeste redusa. Funcția Euler determină cât DEDUCERI din sistemul complet al celor mai mici reziduuri modulo m coprime cu m . Când inactiv m=p avem = p-1.

Definiție. Setul maxim de modulo incomparabil pe perechi m numere coprime cu m , se numește sistem redus de deduceri modulo m. Orice sistem redus de reziduuri modulo m conține elemente, unde este funcția Euler.

Definiție. Orice număr din clasa de echivalență єm vom suna deducere ohm modulo m. Agregat deducere s, luată câte una din fiecare clasă de echivalență єm, se numește sistem complet deducere s modulo m(în sistem complet deducere ov, deci total m bucăți de numere). Direct resturile în sine atunci când sunt împărțite cu m sunt numite cele mai puțin nenegative deducere ami și, desigur, formează un sistem complet deducere s modulo m. Deducere r este numit absolut cel mai mic dacă ïrï este cel mai mic dintre module deducere s din această clasă.

Exemplu. Verificați dacă numerele 13, 8, - 3, 10, 35, 60 formează un sistem complet de reziduuri modulo m=6.

Soluţie: Prin definiție, numerele formează un sistem complet de reziduuri modulo m, dacă sunt exact m dintre ele și sunt modulo incomparabile perechi m.

Incomparabilitatea perechilor poate fi testată prin înlocuirea fiecărui număr cu cel mai mic reziduu nenegativ; dacă nu există repetări, atunci este un sistem complet de deduceri.

Să aplicăm teorema împărțirii cu rest: a = m q + r.

13 = 6 2 + 1 13 1(mod 6); 8 = 6 1 + 2 8 2(mod 6);

3 = 6 (-1) + 3 -3 3(mod 6); 10 = 6 1 + 4 10 4(mod 6);

35 = 6 5 + 5 35 5(mod 6); 60 = 6 10 + 0 60 0 (mod 6).

Am obținut o succesiune de numere: 1, 2, 3, 4, 5, 0, sunt exact 6, nu există repetări și sunt incomparabile pe perechi. Adică formează un sistem complet de reziduuri modulo m = 6.

Exemplu. Înlocuiți cu cea mai mică valoare absolută, precum și cu cel mai mic reziduu pozitiv 185 modulo 16.

Soluţie. Să aplicăm teorema împărțirii cu rest:

185 = 16 11 + 9 185 9 (mod 16).

Exemplu. Verificați dacă se formează numere (13, -13, 29, -9) sistemul redus de reziduuri modulo m=10.

Rezolvare: Orice sistem redus de reziduuri modulo m conține elemente, unde este funcția Euler. În cazul nostru =4, deoarece dintre numerele naturale doar 1, 3, 7, 9 sunt relativ prime cu 10 și nu îl depășesc. Adică, este posibil ca aceste patru numere să alcătuiască sistemul dorit. Să verificăm aceste numere pentru incomparabilitatea lor pe perechi: =4, deoarece dintre numerele naturale doar 1, 3, 7, 9 sunt relativ prime cu 10 și nu o depășesc. Adică, este posibil ca aceste patru numere să alcătuiască sistemul dorit. Să verificăm aceste numere pentru incomparabilitatea lor pe perechi: m .

Opțiunea 1. A= 185, m = 12; Opțiunea 2. a = 84, m = 9;

Opțiunea 3. A= 180, m = 10; Opțiunea 4. a = 82, m = 9;

Opțiunea 5. A= 85, m = 11; Opțiunea 6. a = 84, m = 8;

Opțiunea 7. A= 103, m = 87; Opțiunea 8. a = 84, m = 16;

Opțiunea 9. A= 15, m = 10; Opțiunea 10. a = 81, m = 9;

Opțiunea 11. A= 85, m = 15; Opțiunea 12. a = 74, m = 13;

Opțiunea 13. A= 185, m = 16; Opțiunea 14. a = 14, m = 9;

Opțiunea 15. A= 100, m = 11; Opțiunea 16. a = 484, m = 15;

Opțiunea 17. A= 153, m = 61; Opțiunea 18. a = 217, m = 19;

Opțiunea 19. A= 625, m = 25; Opțiunea 20. a = 624, m = 25;

Sarcina 3. Notați sistemul complet și redus al celui mai mic

Punctul 17. Sisteme complete și reduse de deduceri.

În paragraful anterior, s-a remarcat că raportul єm modulo de comparabilitate m este o relație de echivalență pe mulțimea numerelor întregi. Această relație de echivalență induce o partiție a mulțimii de numere întregi în clase de elemente echivalente, i.e. numerele sunt combinate într-o singură clasă, dând atunci când sunt împărțite la m aceleași resturi. Numărul de clase de echivalență єm(Experții vor spune - „indice de echivalență єm") este exact egal cu m .

Definiție. Orice număr din clasa de echivalență єm se va numi restul modulo m. Set de reziduuri luate câte unul din fiecare clasă de echivalență єm, se numește sistemul complet de reziduuri modulo m(în sistemul complet de deduceri, prin urmare, totalul m bucăți de numere). Direct resturile în sine atunci când sunt împărțite cu m sunt numite resturile cele mai puțin nenegative și, desigur, formează un sistem complet de resturi modulo m. Se spune că un reziduu r este absolut cel mai mic dacă rp este cel mai mic dintre modulele de reziduuri ale clasei date.

Exemplu: Lăsa m= 5 . Apoi:

0, 1, 2, 3, 4 - cele mai mici reziduuri nenegative;

2, -1, 0, 1, 2 sunt absolut cele mai mici reziduuri.

Ambele seturi reduse de numere formează sisteme complete de reziduuri modulo 5 .

Lema 1. 1) Oricare m piese în perechi nu sunt comparabile ca modul m numerele formează un sistem complet de reziduuri modulo m .

2) Dacă Ași m coprim, și Xm, apoi valorile formei liniare topor+b, Unde b- orice număr întreg, de asemenea, rulat prin sistemul complet de reziduuri modulo m .

Dovada. Afirmația 1) este evidentă. Să demonstrăm afirmația 2). Numerele topor+b neted m lucruri. Să arătăm că ele nu sunt comparabile între ele modulo m. Ei bine, lasă pentru unele diferite x 1și x2 din întregul sistem de deduceri a rezultat că ax 1 +b є ax 2 +b(mod m). Apoi, prin proprietățile comparațiilor din paragraful anterior, obținem:

ax 1 - ax 2 (mod m)

x 1 x 2 (mod m)

- o contradicție cu ce x 1și x2 sunt diferite și luate din sistemul complet de deduceri.

Deoarece toate numerele dintr-o clasă de echivalență dată є sunt obținute dintr-un număr dintr-o clasă dată prin adăugarea unui număr care este un multiplu al m, atunci toate numerele din această clasă au modulo m același cel mai mare divizor comun. Din anumite motive, acele deduceri care au cu modulul m cel mai mare divizor comun egal cu unu, i.e. reziduuri care sunt relativ prime față de modul.

Definiție. Sistemul redus de reziduuri modulo m este mulțimea tuturor reziduurilor din sistemul complet coprim cu modulul m .

Sistemul redus este de obicei ales dintre cele mai mici reziduuri nenegative. Este clar că sistemul redus de reziduuri modulo m conține j ( m) bucăți de reziduuri, unde j ( m) este funcția Euler, numărul de numere mai mic decât m si coprime cu m. Dacă până acum ați uitat deja funcția Euler, uitați-vă la paragraful 14 și asigurați-vă că acolo s-a spus ceva despre ea.

Exemplu. Lăsa m= 42. Atunci sistemul redus de reziduuri este:

1, 5, 11, 13, 17, 19, 23, 25, 29, 31, 37, 41.

Lema 2. 1) Orice j ( m) numere care sunt perechi incomparabile modulo mși relativ prim față de modul, formează un sistem redus de reziduuri modulo m .

2) Dacă (a, m) = 1și X trece prin sistemul redus de reziduuri modulo m, apoi topor trece de asemenea prin sistemul redus de reziduuri modulo m .

Dovada. Afirmația 1) este evidentă. Să demonstrăm afirmația 2). Numerele topor sunt incomparabile perechi (acest lucru se dovedește în același mod ca în Lema 1 a acestei subsecțiuni), există exact j ( m) lucruri. De asemenea, este clar că toate sunt relativ prime pentru modul, deoarece (a,m)=1, (x,m)=1 X (ax.m)=1. Deci numerele topor formează sistemul redus de deduceri.

Acestea sunt definițiile și proprietățile de bază ale sistemelor complete și reduse de reziduuri, totuși, în bagajul cunoștințelor matematice există încă o serie de fapte foarte interesante și utile cu privire la sistemele de reziduuri. Dacă păstrăm tăcerea despre ele în acest paragraf, atunci aceasta, mă tem, va fi o încălcare directă a Legii Federației Ruse cu privire la informații, a cărei ascundere rău intenționată, conform acestei legi, este pedepsită administrativ și chiar penal. act. În plus, fără familiarizarea cu alte proprietăți importante ale sistemelor de deducere, punctul 17 se va dovedi a fi foarte scurt. Hai sa continuăm.

Lema 3. Lăsa m 1 , m 2 , ..., m k sunt coprime perechi și m 1 m 2 ...m k =M 1 m 1 =M 2 m 2 =...=M k m k, Unde

1) Dacă x 1 , x 2 , ..., x k rulează prin sisteme complete de reziduuri modulo m 1 , m 2 , ..., m k parcurge sistemul complet de reziduuri modulo m=m 1 m 2 ...m k .

2) Dacă x 1 , x 2 , ..., x k parcurge sistemele reduse de reziduuri modulo m 1 , m 2 , ..., m k respectiv, apoi valorile formei liniare parcurge sistemul redus de reziduuri modulo m=m 1 m 2 ...m k .

Dovada.

1) Forma M1x1 +M2x2 + ...+Mkxk evident ia m 1 m 2 ...m k =m valorile. Să arătăm că aceste valori sunt incomparabile în perechi. Ei bine, lasă

M 1 x 1 +M 2 x 2 + ...+M k x k є M 1 x 1 C +M 2 x 2 C + ...+M k x k C (mod m)

Orice Mj, diferit de Domnișoară, multiple Domnișoară. Eliminarea termenilor din stânga și din dreapta din ultima comparație, multipli de Domnișoară, primim:

M s x s є M s x s C (mod m s) Yu x s ​​​​є x s C (mod m s)

- o contradicție cu ce x s parcurge sistemul complet de reziduuri modulo Domnișoară .

2). Forma M1x1 +M2x2 + ...+Mkxk evident ia j ( m 1) j ( m2) Ch ... Ch j ( m k) = j ( m 1 m 2 W ... W m k)= j ( m) (funcția Euler este multiplicativă!) de diferite valori, care modulo m=m 1 m 2 ...m k perechi incomparabil. Acesta din urmă se dovedește cu ușurință prin argumente asemănătoare celor folosite în demonstrația aserției 1) a acestei leme. Pentru că ( M 1 x 1 +M 2 x 2 + ...+M k x k ,m s)=(M s x s ,m s)=1 pentru toată lumea 1 J s J k, apoi ( M 1 x 1 +M 2 x 2 + ...+M k x k ,m s)=1, de unde și setul de valori ale formei M1x1 +M2x2 + ...+Mkxk formează un sistem redus de reziduuri modulo m .

Lema 4. Lăsa x 1 , x 2 , ..., xk ,x alerga plin și x 1 , x 2 ,..., x k , x– rulează prin sistemele reduse de reziduuri în module m 1 , m 2 , ..., m kși m=m 1 m 2 ...m k respectiv, unde (m i m j)=1 la i № j. Apoi fracții potrivire cu fracții (x/m), și fracții potrivire cu fracții (x/m) .

Dovada. Dovada ambelor afirmații ale Lemei 4 se obține ușor prin aplicarea Lemei 3 anterioare după ce ați dat fiecare sumă (x 1 /m 1 +x 2 /m 2 +...+x k /m k )și ( x 1 /m 1 + x 2 /m 2 +...+ x k /m k ) la un numitor comun:

(x 1 /m 1 +x 2 /m 2 +...+x k /m k )=((M 1 x 1 +M 2 x 2 +...+M k x k)/m) ;

( x 1 /m 1 + x 2 /m 2 +...+ x k /m k )=((M 1 x 1 +M 2 x 2 +...+M k x k)/m) ,

Unde M j =m 1 ...m j-1 m j+1 ...m k .

Dacă acum luăm în considerare că părțile fracționale ale numerelor obținute prin împărțirea la modulo m oricare două numere comparabile ca modul m, sunt la fel (sunt egale r/m, Unde r este cel mai mic reziduu nenegativ din clasa dată), atunci afirmațiile prezentei leme devin evidente.

În restul acestei secțiuni, se va întâmpla cel mai interesant lucru - vom însuma rădăcinile complexe m puterea de la unitate și vom descoperi conexiuni uimitoare între sumele rădăcinilor, sistemele de reziduuri și funcția Möbius multiplicativă deja familiară m ( m) .

Se notează cu e k k-a rădăcină m- oh grad de unitate:

Ne amintim bine aceste forme de scriere a numerelor complexe din primul an. Aici k=0,1,...,m-1– parcurge sistemul complet de reziduuri modulo m .

Amintiți-vă că suma e 0 + e 1 +...+ e m-1 toate rădăcinile m Puterea unității este zero pentru oricare m. Într-adevăr, să e 0 + e 1 +...+ e m-1 =a. Să înmulțim această sumă cu un număr diferit de zero e 1 . O astfel de multiplicare geometrică în plan complex înseamnă rotirea corectului m-gon, la vârfurile cărora se află rădăcinile e 0 , e 1 ,..., e m-1, la un unghi diferit de zero 2p/m. Este clar că în acest caz rădăcina e 0 mergi la root e 1, rădăcină e 1 mergi la root e 2, etc., și rădăcina e m-1 mergi la root e 0, adică sumă e 0 + e 1 +...+ e m-1 Nu se va schimba. Avem e 1 a=a, Unde a=0 .

Teorema 1. Lăsa m>0- un număr întreg, un O Z , X parcurge sistemul complet de reziduuri modulo m. Atunci dacă A multiplu m, apoi

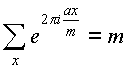
altfel, când A nu un multiplu m ,

.

Dovada. La A multiplu m avem: a=mdși

La A nedivizibil cu m, împărțiți numărătorul și numitorul fracției a.m pe d este cel mai mare divizor comun Ași m, obținem o fracție ireductibilă a 1 /m 1. Apoi, după Lema 1, a 1 x va rula prin sistemul complet de reziduuri modulo m. Avem:

deoarece suma tuturor rădăcinilor gradului m 1 de la unitate este egal cu zero.

Amintiți-vă că rădăcina e k m a-a putere a unității se numește antiderivată dacă indicele ei k reciproc simplu cu m. În acest caz, după cum s-a dovedit în primul an, grade succesive e k 1 , e k 2 ,..., e k m-1 rădăcină e k formează întregul set de rădăcini m puterea din unitate sau, cu alte cuvinte, e k este un generator al grupului ciclic al tuturor rădăcinilor m gradul de la unitate.

Evident, numărul de rădăcini primitive diferite m Puterea unității este egală cu j ( m), unde j este funcția Euler, deoarece indicii rădăcinilor primitive formează un sistem redus de reziduuri modulo m .

Teorema 2. Lăsa m>0 este un număr întreg, x trece prin sistemul redus de reziduuri modulo m. Apoi (suma rădăcinilor primitive ale gradului m):

unde m ( m) este funcția Möbius.

Dovada. Lăsa m=p 1 a 1 p 2 a 2 ...p k a k este extinderea canonică a numărului m ; m 1 \u003d p 1 a 1 , m 2 \u003d p 2 a 2 , m 3 \u003d p 3 a 3; x i trece prin sistemul redus de reziduuri modulo m i. Avem:

La a s = 1 rezultă că doar rădăcina e 0 =1 nu este primitiv, deci suma tuturor rădăcinilor primitive este suma tuturor rădăcinilor minus unu:

astfel, dacă m fără pătrate (adică nu este divizibil cu r2, la r>1), apoi

Dacă vreun indicator la fel de mai mare decât unu (adică m impartit de r2, la r>1), apoi suma tuturor rădăcinilor primitive ale gradului Domnișoară este suma tuturor rădăcinilor gradului Domnișoară minus suma tuturor rădăcinilor neprimitive, adică toate rădăcinile într-o oarecare măsură mai puțin Domnișoară. Exact, dacă m s =p s m s *, apoi:

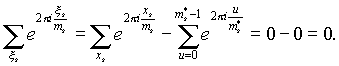
Acum, dragi cititori, când v-am prezentat în atenția dumneavoastră o cantitate destul de semnificativă de informații despre sistemele de deducere complete și reduse, nimeni nu mă poate acuza că am încălcat cu răutate Legea Informației a Federației Ruse prin reținerea acesteia, așa că închei asta. paragraf cu satisfacție.

puzzle-uri

1 . Notați pe o bucată de hârtie toate cele mai mici reziduuri nenegative și toate cele mai mici reziduuri absolut a) modulo 6, b) modulo 8. Chiar mai jos, notați sistemele date de deduceri pentru aceste module. Desenați separat pe planul complex rădăcinile rădăcinilor a șasea și a opta a unității, în ambele figuri încercuiți rădăcinile primitive și găsiți în fiecare caz suma lor. 2 . Lăsa e- rădăcină primitivă 2n dintr-o unitate. Găsiți suma: 1+ e + e 2 +...+ e n-1 . 3 . Aflați suma tuturor rădăcinilor primitive: a) a 15-a; b) 24; c) gradul 30 de la unitate. 4 . Aflați suma tuturor produselor posibile ale rădăcinilor primitive n gradul de la unu, luat de doi. 5 . afla suma k-x puterile tuturor rădăcinilor n gradul de la unitate. 6 . Lăsa m>1 , (a, m)=1 , b este un număr întreg, X trece prin sistemul complet și x trece prin sistemul redus de reziduuri modulo m. Demonstrați că: A) b) 7 . Demonstrați că: , Unde R trece prin toți divizorii primi ai unui număr A .

Sistem complet de facturare. Sistemul dat de deduceri. Cele mai comune sisteme deductive sunt: ​​cel mai puțin pozitiv, cel mai puțin nenegativ, absolut cel puțin etc.

Teorema 1. Proprietăți ale sistemului complet și redus de reziduuri.

1°.Criterii pentru un sistem complet de deduceri. Orice combinație de m numere întregi care sunt modulo incomparabile pe perechi m, formează un sistem complet de reziduuri modulo m.

2°. Dacă numerele X 1 , X 2 , ..., x m– sistem complet de reziduuri modulo m, (A, m) = 1, b este un întreg arbitrar, apoi numerele topor 1 +b, topor 2 +b, ..., topor m+b constituie de asemenea un sistem complet de reziduuri modulo m.

3°. Criteriul sistemului de reducere redusă. Orice colecție constând din j( m) numere întregi care sunt modulo incomparabile pe perechi mși coprim cu modulul, formează un sistem redus de reziduuri modulo m.

4°. Dacă numerele X 1 , X 2 , ..., X j ( m) este sistemul redus de reziduuri modulo m, (A, m) = 1, apoi numerele topor 1 , topor 2 , ..., un x j ( m) constituie de asemenea sistemul redus de reziduuri modulo m.

Teorema 2. teorema lui Euler.

Dacă numerele Ași m coprim, atunci A j ( m) º 1(mod m).

Consecinţă.

1°. teorema lui Fermat. În cazul în care un p este un număr prim și A nedivizibil cu p, apoi a p–1 º 1 (mod p).

2°. Teorema lui Fermat generalizată. În cazul în care un p atunci este un număr prim a p º A(mod p) pentru orice AÎ Z .

§ patru. Rezolvarea comparațiilor cu o variabilă

Decizia de comparare. Echivalenţă. Gradul de comparație.

Teorema. Proprietăți ale soluțiilor de congruențe.

1° Soluțiile de congruențe sunt clase întregi de reziduuri.

2°. (" k)(un k º b k(mod m))Ù k= z al comparației º 0 (mod m) și º 0 (mod m) sunt echivalente.

3°. Dacă ambele părți ale comparației sunt înmulțite cu un număr coprim cu modulul, atunci se obține o comparație care este echivalentă cu cea inițială.

4°. Orice comparație modulo un prim p echivalează cu o comparație, al cărei grad nu depășește p–1.

5°. Comparație º 0 (mod p), Unde p este un număr prim, are cel mult n diverse solutii.

6°. teorema lui Wilson. ( n-unu)! º –1 (mod n) Û n Număr prim.

§ 5. Rezolvarea comparatiilor de gradul I

topor º b(mod m).

Teorema. 1°. În cazul în care un ( A, m) = 1, atunci comparația are o soluție și este unică.

2°. În cazul în care un ( A, m) = dși b nedivizibil cu d, atunci comparația nu are soluții.

3°. În cazul în care un ( A, m) = dși b impartit de d, atunci comparația are d diferite soluții care alcătuiesc o clasă de resturi modulo.

Modalități de rezolvare a comparațiilor topor º b(mod m) când ( A, m) = 1:

1) selecția (enumerarea elementelor unui sistem complet de deduceri);

2) utilizarea teoremei lui Euler;

3) utilizarea algoritmului Euclid;

4) variația coeficienților (folosind proprietatea 2° a sistemului complet de reziduuri din Teorema 2.2);

§6. Ecuații nedefinite de gradul I

topor+de = c.

Teorema. Ecuația topor+de = c rezolvabil dacă și numai dacă c (A, b).

Cand ( A, b) = 1 toate soluțiile ecuației sunt date prin formule

tÎ Z , Unde X 0 este o soluție de comparație

topor º c(mod b), y 0 = .

Ecuații diofantine.

CAPITOLUL 10. Numere complexe

Definirea unui sistem de numere complexe. Existența unui sistem de numere complexe

Definirea unui sistem de numere complexe.

Teorema. Sistemul de numere complexe există.

Model: R 2 cu operatii

(A, b)+(c, d) = (A+c, b+d), (A, b)×( c, d) = (ac–bd, bc+anunț),

i= (0, 1) și identificare A = (A, 0).

Forma algebrică a unui număr complex

Reprezentarea unui număr complex în formă z = A+bi, Unde A, bÎ R , i 2 = -1. Unicitatea unei astfel de reprezentări. Re z, Sunt z.

Reguli pentru efectuarea operaţiilor aritmetice asupra numerelor complexe în formă algebrică.

Aritmetic n-spațiu vectorial dimensional C n. Sisteme de ecuații liniare, matrice și determinanți peste C .

Extragerea rădăcinilor pătrate din numere complexe în formă algebrică.
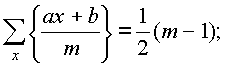